RTI指标的Python实现：更精确地识别超买超卖、确认趋势和捕捉反转信号

RTI是什么？

相对趋势指数（RTI）是一种用于衡量市场趋势强度和方向的技术分析工具。RTI具有独特的适应性和对市场波动的响应能力，并且尽量减少次要的、短期的市场波动的影响。它将趋势跟踪和均值回归特征结合在一起，提供了可定制和直观的趋势强度方法。RTI对价格行为的敏感性使其表现十分突出。

相对强弱指数（RSI）和相对趋势指数（RTI）都是强大的技术指标，但它们各自具有一些差异。RTI在识别趋势和超买/超卖（OB/OS）区域方面更加精细和准确。RSI是一种用于衡量价格变动速度和变化的动量震荡器，通常用于识别市场中的超买和超卖状态。然而，RSI的主要局限性是在持续趋势期间容易产生虚假信号。相比之下，RTI专门设计用于识别和适应市场趋势。RTI不仅关注价格变动，还测量当前收盘价在最近范围内的相对位置，提供了更全面的市场状况视角。RTI的适应性特点非常有价值。交易者可以调整指标的响应性，以更好地适应突发市场波动和噪音，从而减少产生虚假信号的可能性。这个特性使得RTI在各种市场条件下都有优势，无论是趋势行情还是震荡和横盘行情。此外，RTI采用了一种独特的方法来定义OB/OS区域，考虑了当前趋势，可以更精确地反映市场状态。

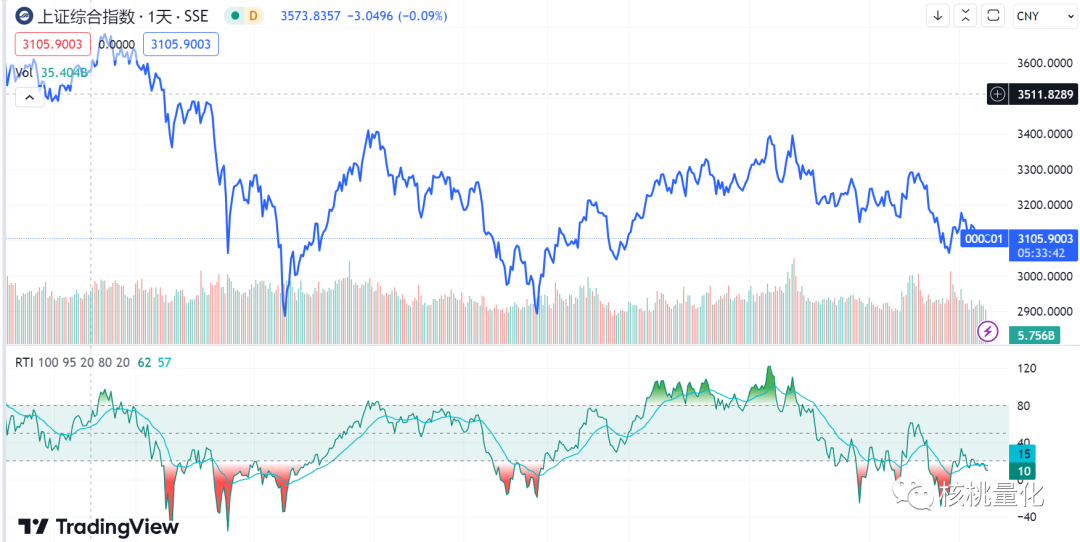
如何计算RTI?

RTI的数学原理基于标准差和百分位数这两个基本统计概念:

• 标准差是用来衡量数据集中分散性或变异性的度量。在RTI中，我们使用标准差来计算指定时间段内收盘价格的波动情况。标准差越高，代表价格波动越大。
• 百分位数是用于表示给定观察值在整个数据集中所处位置的统计度量。在计算上限和下限趋势时，RTI使用百分位数来从排序后的数组中提取值。通过调整百分位数（通过”灵敏度”参数控制），我们可以决定是只对极端事件做出反应还是更积极地反应并将较小偏差视为显著。

最后，RTI计算出一个相对趋势指数值，该值标准化了当前价格在上限和下限趋势之间的位置。这个比率提供了一种标准化的衡量标准，可用于识别潜在的交易信号。

RTI的核心组件包括趋势数据计数和趋势敏感度百分比。趋势数据计数决定了在RTI计算中使用的数据点数量，即趋势的长度。较高的计数可以捕捉更广泛的市场视野（长期趋势），提供更平滑的结果，对突然的市场变化有更强的抵抗能力。相反，较低的计数侧重于更新的数据（短期趋势），能更快地响应市场变化，但对市场噪音更敏感。趋势敏感度百分比用于选择趋势数组中用于定义上限和下限趋势的索引。通过调整该参数，用户可以影响趋势的敏感度，较高的百分比表示趋势更不敏感。

如何使用RTI指标？

RTI是一种技术指标，用于分析市场趋势和判断超买超卖情况。RTI通常围绕50进行震荡。当RTI值高于50时，表示市场趋势看涨（向上），当低于50时，表示市场趋势看跌（向下）。而且，RTI偏离50线越远，趋势就越强。

RTI还包括用户定义的超买和超卖水平。当RTI值超过超买水平或低于超卖水平时，表示可能存在交易机会，提示交易者买入或卖出。除了作为趋势跟踪指标，RTI还可以用作均值回归工具。RTI可以用于以下方面：

• 趋势确认和反转：如果RTI值持续接近上限，可能表示强劲的上升趋势；相反，如果接近较低水平，可能表示下降趋势。如果RTI值开始从一个趋势线转向另一个趋势线，可能表明潜在的趋势逆转。
• 识别超买和超卖情况：当RTI值达到上趋势线时，表示可能存在超买情况，即价格已被推高过高，并且可能会出现回调或强劲的积极趋势。相反，当RTI值触及较低趋势线时，表示可能存在超卖情况，即价格可能已被压低并可能会反弹，或者表示强烈的负面趋势。交易者经常将这些超买和超卖信号视为反向指标，认为它们是卖出（在超买条件下）或买入（在超卖条件下）的潜在迹象。如果RTI线在较长时间内保持超买或超卖状态，表示该方向存在强劲趋势。

在参数设置方面，RTI具有可配置性。用户可以设置趋势数据长度和趋势敏感度。

• 趋势数据长度表示用于计算趋势的数据点数量。较长的趋势数据长度可以反映更长期的趋势，而较短的趋势数据长度可以捕捉短期变动。
• 趋势敏感度指定了构成显著趋势的阈值。较高的敏感度水平会认为较小的价格变动具有重大意义，从而使趋势不太敏感。相反，较低的敏感度水平会认为更多的价格变动是重要的，从而使趋势更加敏感。

使用Python实现RTI指标计算？

下面是RTI指标的Python实现，原始实现参考[1] 。

import math
import numpy as np
import pandas as pd
from numpy.lib.stride_tricks import as_strided

def sliding_window(arr, window_size, fill_value=np.nan):
    """
    滑动窗口函数，用于从一个一维Numpy数组中提取所有长度为window_size的子数组。

    参数：
    arr: 一维Numpy数组，表示要提取子数组的原始数组。
    window_size: 整数，表示子数组的长度。
    fill_value: 用于填充数组的值。默认为np.nan。

    返回值：
    一个二维Numpy数组，表示所有长度为window_size的子数组。其中，每一行表示一个子数组。
    """
    # 在原始数组前面添加填充值
    padded_arr = np.concatenate([np.full((window_size-1), fill_value), arr])
    nrows = arr.shape[0]
    row_stride, = padded_arr.strides
    # 创建视图数组，避免复制数据
    result = as_strided(padded_arr, shape=(nrows, window_size), strides=(row_stride, row_stride))
    return result

def sliding_window_std(arr, window_size):
    """
    计算滑动窗口的标准差。

    参数：
    arr: 一维Numpy数组，表示要计算标准差的原始数组。
    window_size: 整数，表示滑动窗口的大小。

    返回值：
    一个一维Numpy数组，表示每个滑动窗口的标准差。其中，每个元素表示一个滑动窗口的标准差。
    """
    subarrays = sliding_window(arr, window_size)
    stds = np.std(subarrays, axis=1)
    return stds

def ema(source, length):
    """
    计算指数加权移动平均线EMA。

    参数：
    source: 一维Python列表或Numpy数组，表示输入数据。
    length: 整数，表示EMA的时间周期。

    返回值：
    一个一维Numpy数组，表示EMA值。其中，每个元素表示对应位置的EMA值。
    """
    alpha = 2 / (length + 1)
    ema_list = []
    for i in range(len(source)):
        if i == 0:
            ema_list.append(source[0])
        else:
            if math.isnan(ema_list[-1]):
                ema_i = source[i]
            else:
                ema_i = alpha * source[i] + (1 - alpha) * ema_list[-1]
            ema_list.append(ema_i)
    return np.array(ema_list)

def relative_trend_index(data,
                         trend_window=100,
                         std_window=2,
                         ma_window=20,
                         trend_sensitivity_percentage=95,
                         trend_data_count=100):
    """
    计算相对趋势指数（Relative Trend Index，RTI）。

    参考：https://www.tradingview.com/script/VwmUNNwp-Relative-Trend-Index-RTI-by-Zeiierman/

    参数：
    data: 一维Numpy数组，表示要计算RTI的原始数据。
    trend_window: 整数，表示计算上下趋势线的滑动窗口大小。默认为100。
    std_window: 整数，表示计算标准差的滑动窗口大小。默认为2。
    ma_window: 整数，表示计算移动平均值的滑动窗口大小。默认为20。
    trend_sensitivity_percentage: 整数，表示上下趋势线的敏感度百分比。默认为95。
    trend_data_count: 整数，表示用于计算上下趋势线的数据点数量。默认为100。

    返回值：
    一个一维Numpy数组，表示RTI。其中，每个元素表示原始数据中对应位置的RTI值。
    """
    index = data.index
    data = data.values
    # 计算滑动窗口标准差
    std_dev = sliding_window_std(data, std_window)
    # 计算上下趋势线
    upper_trend = data + std_dev
    lower_trend = data - std_dev
    # 提取所有长度为trend_window的子数组
    upper_array = sliding_window(upper_trend, trend_window)
    lower_array = sliding_window(lower_trend, trend_window)
    # 对每一行按升序排序
    upper_array = np.take_along_axis(upper_array, np.argsort(upper_array, axis=1), axis=1)
    lower_array = np.take_along_axis(lower_array, np.argsort(lower_array, axis=1), axis=1)
    # 计算上下趋势线的索引
    upper_index = round(trend_sensitivity_percentage / 100 * trend_window) - 1
    lower_index = round((100 - trend_sensitivity_percentage) / 100 * trend_window) - 1
    # 提取上下趋势线
    UpperTrend = upper_array[:, upper_index]
    LowerTrend = lower_array[:, lower_index]
    # 计算RTI
    rti = ((data - LowerTrend) / (UpperTrend - LowerTrend)) * 100
    ma_rti = ema(rti, ma_window)
    rti = ema(rti, int(ma_window/2))
    result = pd.DataFrame({"rti":rti,"ma_rti":ma_rti},index=index)

    return result