量化paper读书笔记（四）—— AIPGS-基于AI的股票分组系统

本文概述

本文探讨了如何利用AI开发一个数据驱动的股票分组系统，以捕捉市场感知，从而将公司按照不同粒度水平分组。文中介绍了一种连续的公司相似性度量方法，并使用该方法将公司分组并构建对冲投资组合。研究表明，相同集群中的公司具有较强的同质风险和回报特征，而不同集群中的公司则具有不同的风险暴露。本文还开发了一个交互式可视化系统，用于识别基于人工智能的集群和相似公司。

本文亮点

1. 数据驱动的行业同业分组系统：通过人工智能技术从多种数据源中提取特征并学习关系的方法，能够根据市场感知将公司进行分组。

2. 相似性度量和对冲投资组合：一种连续的相似性度量方法，并利用这种方法将公司分组，并展示了如何利用这些分组来构建对冲投资组合。

3. 高同质性和多样性：研究发现，基于该方法分组的公司在样本外期的回报相关性较高，但稳定性和可解释性较低。

4. 交互式可视化工具：文章还开发了一个用于可视化基于人工智能的集群和相似公司的交互式工具。

本文主线

本文从数据到模型搭建再到最终的组合主要可分为4个步骤：

1. 数据获取（Data）：

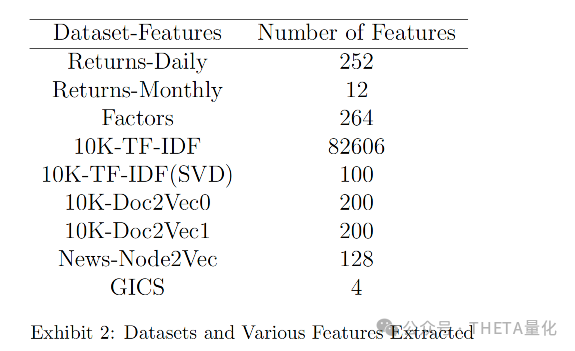
   • 股票回报、因子暴露、10-K报告、新闻共同提及以及GICS（全球行业分类系统）分组数据数据。
2. 特征提取（Feature Extraction）:
   • 通过不同的方法提取特征，例如使用术语频率-逆文档频率（TF-IDF）和Doc2Vec处理10-K报告文件，以及使用Node2Vec处理新闻提及，以捕捉公司间的潜在相似性。
3. 距离度量（Distance Metrics）:
   • 利用机器学习（ML）模型处理特征数据，预测公司间未来的回报相关性，这被视为市场感知的代理变量。
   • 使用余弦相似度和ML度量计算公司间的相似性得分，这些模型处理t年结束时的数据，预测并估计t+1年公司间基于回报相关性的距离。
4. 聚类（Clustering）:
   • 使用层次聚类方法将公司分组为相似公司的集合。层次聚类是一种自底向上的方法，逐步合并相似的公司，形成不同层级的行业分组。
   • 利用Ward方法作为链接准则，最小化聚类内部的方差，以形成大小相似的聚类。

步骤拆解

下面是对于上文提到的4个主体步骤进行展开：

1. 数据获取

• 收集了所有公司的日常和月度回报数据。
• 根据MSCI Barra美国全市场模型，使用了描述性因子暴露数据。
• 使用10-K报告中的业务描述部分，这部分包含了公司业务和运营的详细信息。
• 从Ravenpack获取公司在新闻文章中共同提及的信息。
• GICS是一个市场导向的行业标准分类系统，用于金融公司和全球投资者。

2. 特征提取

1. 股票回报（Returns）:
   • 使用股票回报的相关性来量化公司间的相似性，因为同一行业内的公司通常会经历相似的市场冲击。
2. 因子暴露（Factor Exposures）:
   • 因子暴露包括慢速变化因子（如销售额的变异性）和快速变化因子（如短期反转）。
3. 10-K报告文件（10-K Filings）:
   • TF-IDF (Term Frequency-Inverse Document Frequency): 用于确定文档中最重要的词汇，通过词汇频率和逆文档频率的乘积来表示。
   • Doc2Vec: 一种无监督学习方法，用于获取文档嵌入，为每份10-K文件生成两个表示（Doc2Vec0和Doc2Vec1）。
4. 新闻共同提及（News Co-Mentions）:
   • 共现（Co-occurrence）: 计算每对公司在新闻文章中共现的Jaccard相似度。
   • Node2Vec: 捕捉公司间的更高级别联系，构建了一个图，其中公司是节点，共同提及的公司通过边连接，边的权重由文章中提及公司对的次数决定。
5. GICS分组数据（GICS）:
   • 除了作为基线分类系统外，GICS数据也被用作相似性预测模型的一个输入。

在特征提取过程中，使用了不同的数据处理技术来降低数据维度并提取关键信息，例如对TF-IDF特征使用截断奇异值分解（SVD）将维度降低到100。这些特征随后被用于机器学习模型来预测公司间的未来回报相关性。

3. 距离度量

该部分部分展示了如何使用机器学习（ML）模型来预测公司间基于特征的未来回报相关性，并将其作为公司间相似性的度量。

1. 相似性特征向量构建:
   • 对于每对公司，基于不同数据集的特征，构建了一个相似性特征向量。这个向量通过连接不同特征向量之间的L1距离和余弦相似度来形成。
   • 具体来说，给定两个公司i和j的特征向量𝑓𝑖𝑘和𝑓𝑗𝑘，相似性特征向量𝐹𝑖,𝑗由以下公式构成：

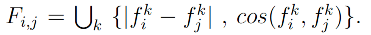
1. • 这里的𝑓表示特征向量，i和j代表公司，而k可能代表不同的数据集，如月度回报、日常回报、10-K-TF-IDF(SVD)、10K-Doc2Vec或新闻Node2Vec特征。
2. 余弦相似度和L1距离:
   • 使用余弦相似度和L1距离来量化特征向量之间的相似性和差异性。
   • 余弦相似度测量了两个向量在方向上的相似性，而L1距离（即曼哈顿距离）测量了它们在空间中的实际距离。
3. 机器学习模型:
   • 岭回归（Ridge Regression）：一种带有L2正则化的线性回归模型，用于预测公司间的相似性。
   • 神经网络（Neural Networks）：非线性模型，用于捕捉输入特征和输出之间的复杂关系。
   • XGBoost：一种梯度增强的决策树模型，通过组合多个弱模型（决策树）来构建一个强预测模型。
4. • 使用了多种机器学习模型来学习特征向量之间的关系，并预测公司间的未来回报相关性。
5. 训练和验证:
   • 训练数据由样本中所有公司对的相似性特征向量组成。
   • 对于测试年份𝑡+1（即出样本时期），使用年份𝑡−1的训练数据，并在年份𝑡进行验证。
   • 一旦机器学习模型被训练并且超参数被调整后，它被用来获取出样本年份𝑡+1所有公司对的相似性得分。
6. 相似性得分的应用:
   • 使用预测的相似性得分来确定每对公司之间的距离，这个距离是通过(1−SimilarityScore)(1−SimilarityScore)来计算的。
   • 这些相似性得分随后被用于层次聚类分析，以形成相似公司的群组。

4. 聚类

1. 层次聚类（Hierarchical Clustering）:
   • 文章采用了层次聚类方法，这是一种自底向上（agglomerative）的聚类技术，它从将每个公司视为一个独立聚类开始，逐步合并最相似的聚类对。
2. 距离计算:
   • 使用ML模型预测的相似性得分来计算公司间的成对距离。距离是通过(1−SimilarityScore)(1−SimilarityScore)转换得到的，其中相似性得分越低，表示公司间的差异越大，距离越远。
3. 链接方法（Linkage Method）:
   • 文章中使用了Ward’s方法作为链接准则，该方法通过最小化聚类内部的方差来合并聚类，即最小化合并后聚类中心的变化。这有助于创建大小相似的聚类。
4. 聚类层级（Cluster Hierarchy）:
   • 聚类层级对应于不同的行业分组级别，如行业（sector）、行业组（industry group）和子行业（sub-industry）。
   • 为了与GICS分类系统进行公平比较，层次聚类的聚类数量被设定为与GICS在每个层级上的聚类数量大致相等。
5. 聚类稳定性（Cluster Stability）:
   • 文章还考虑了聚类的稳定性，即在连续年份间聚类成员的变化程度。稳定性是通过计算连续年份中保持相同聚类成员的聚类所占的百分比来评估的。
6. 聚类评估（Cluster Evaluation）:
   • 聚类结果的有效性通过评估聚类内公司间的平均未来回报相关性（平均相关系数）来确定。如果聚类内公司间具有较高的平均相关系数，则表明聚类是有效的。
7. 聚类数量（Number of Clusters）:
   • 文章中提到，层次聚类可以用来获得任意数量的聚类，但在与GICS比较时，作者选择了与GICS聚类数量大致相等的聚类数。
8. 聚类结果的应用:
   • 聚类结果用于不同的应用，例如投资组合构建、对冲策略和其他领域。聚类可以帮助投资者识别具有相似风险-回报特征的公司群体。
9. 可视化工具（Visualization Tools）:
   • 文章还开发了一个交互式可视化系统，用于识别基于AI的聚类和相似公司。这个工具可以帮助投资者更直观地理解聚类结果。

实验结果

结果显示，AIPGS在多个关键指标上超越了现有的行业分类系统，尤其是与全球行业分类系统（GICS）相比。AIPGS利用机器学习模型，通过分析公司的历史数据和市场行为，预测公司间的未来回报相关性，并据此进行聚类。这种方法使得AIPGS能够动态地更新行业分组，以反映市场对公司认知的变化。

性能评估指标：

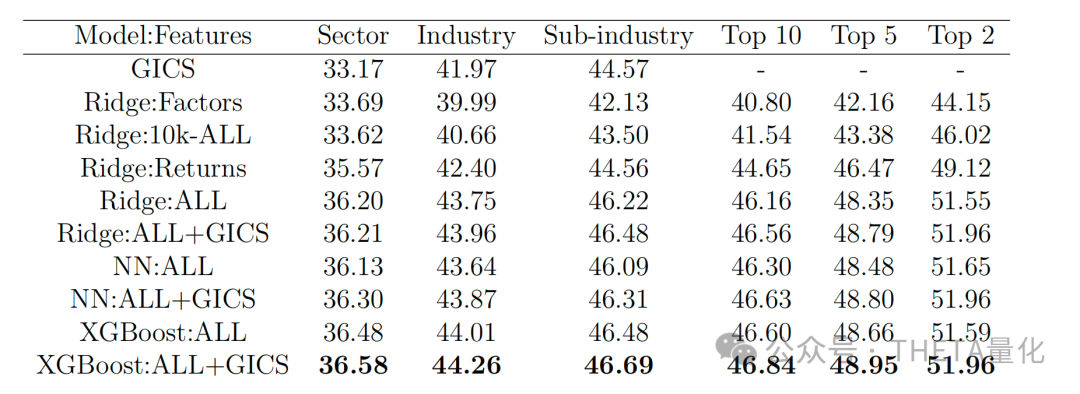
下表展示了基于机器学习模型得到的聚类的平均回报相关性。此表显示，与GICS聚类相比，机器学习聚类在行业和子行业级别上的平均回报相关性有显著提高。

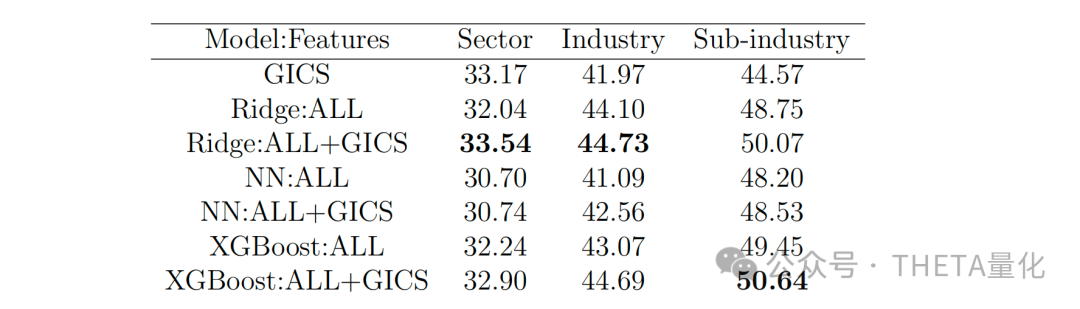
下表展示了机器学习聚类与GICS聚类之间的相似性，通过调整Rand指数（ARI）来衡量。此表显示，当将GICS特征作为输入时，机器学习聚类与GICS的相似性显著提高。

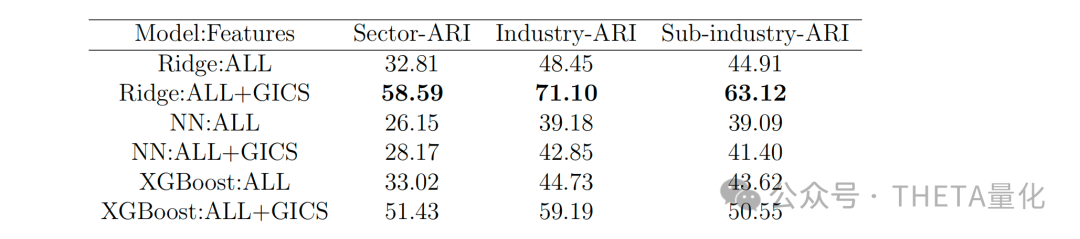
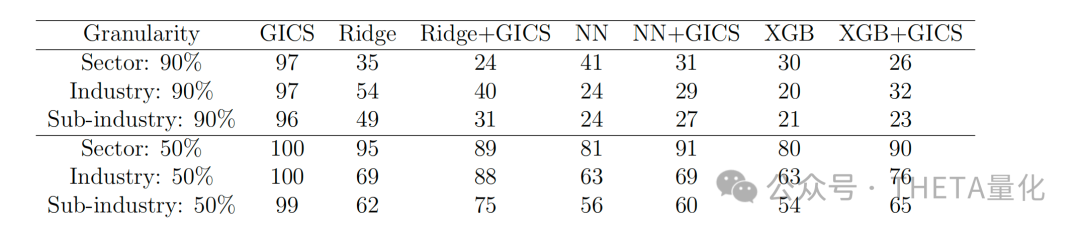
下表展示了不同聚类方法的稳定性，包括保留90%和50%公司的比例。此表显示，尽管AIPGS聚类是动态的，但它们在不同年份之间保持了相当的稳定性。

下表展示了聚类因子回报的分散性，作为衡量聚类在投资组合构建中分散化潜力的指标。可以看出机器学习聚类的跨截面分散性比GICS聚类高出30%。

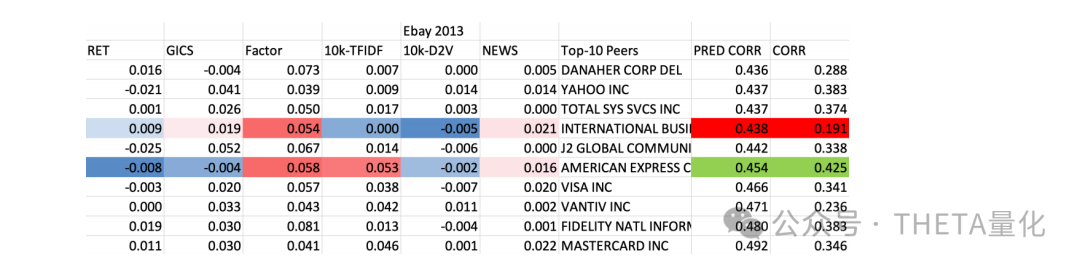
下表展示了使用不同模型选择的同行公司对冲单一股票投资组合风险暴露的效果。与基于GICS的同行公司相比，使用机器学习模型选择的同行公司能够显著降低对冲组合的实现波动性（realized）。

模型解释：

XGBoost是一种梯度增强决策树模型，它通过结合多个弱模型（决策树）来构建一个强模型。尽管单独的决策树是可解释的，但当它们结合在一起时，整个模型的解释性就变得复杂。为了解决这个问题，作者使用了TreeSHAP方法，这是一种事后解释性方法，通过计算特征的Shapley值来确定它们对模型输出的贡献。

结论