之前的文章《寻求平衡:兼顾高收益与低波动的轮动策略》分享了一个基于创业板动量成长指数和中证红利低波动指数的轮动策略,策略的累计回报率高达385%,夏普比率为1.43,年化回报率高达38%。由于指数是不能直接持有的,本文基于上述策略分享一个对应指数跟踪的ETF交易策略,策略在整个回测过程中夏普比率为1.64,年化回报率高达44%。
创业板动量成长指数是由中证指数有限公司编制的,选取创业板市场中具有良好成长能力和动量效应的50只股票组成的指数,对应的指数代码为399296,该指数的跟踪基金为创成长ETF(场内基金代码: 159967)。中证红利低波动指数是中证指数有限公司编制的一种反映市场上分红水平高且波动率低的证券整体表现的指数,对应的指数代码为H30269,该指数的跟踪基金为红利低波ETF(场内基金代码: 512890)。
策略描述
该策略的基本思想是始终持有过去一段时间涨幅大的资产,在两种资产间进行轮动。这样可以在红利低波指数的稳健性和创成长指数的高收益之间寻求平衡。
构建步骤:
-
选择创成长ETF和红利低波ETF作为投资组合的标的指数。 -
每日计算两种指数过去21个交易日(含计算当日)的涨跌幅。 -
比较两类ETF的涨幅,选择涨幅更大的ETF作为投资标的。 -
根据涨幅更大的指数,以当日收盘价买入对应的ETF基金。 -
持有所购买的ETF基金,直到下一个调仓日。 -
每个调仓日重复以上步骤,根据涨幅更大的指数进行轮动投资。
代码实现
#!pip install akshare quantstats
import warnings
warnings.filterwarnings('ignore')
import time
import akshare as ak
import numpy as np
import pandas as pd
import quantstats as qs
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
# %matplotlib inline
# 获取 ETF 历史数据
etf_1 = ak.fund_etf_hist_em(symbol="159967", period="daily", adjust="hfq")[["日期","收盘"]] \
.rename(columns={"日期":"date","收盘":"etf_1"}).set_index("date")
etf_2 = ak.fund_etf_hist_em(symbol="512890", period="daily", adjust="hfq")[["日期","收盘"]] \
.rename(columns={"日期":"date","收盘":"etf_2"}).set_index("date")
# 合并数据
data = pd.concat([etf_1, etf_2], axis=1).dropna().iloc[:]
data.index = pd.to_datetime(data.index)
# 计算每日涨跌幅和滚动收益率
data["etf_1_day_return"] = data.etf_1.rolling(2).apply(lambda x:(x[-1]-x[0])/x[0])
data["etf_2_day_return"] = data.etf_2.rolling(2).apply(lambda x:(x[-1]-x[0])/x[0])
data["etf_1_return"] = data.etf_1.rolling(window=21).apply(lambda x: x[-1]/x[0])
data["etf_2_return"] = data.etf_2.rolling(window=21).apply(lambda x: x[-1]/x[0])
# 去掉缺失值
data = data.dropna()
# 生成交易信号和收益率
data["signal"] = data["etf_1_return"] > data["etf_2_return"]
data["signal"] = data["signal"].shift(1)
data = data.dropna()
data["etf_1_return"] = (100/data["etf_1"].values[0]) * data["etf_1"]
data["etf_2_return"] = (100/data["etf_2"].values[0]) * data["etf_2"]
data["signal_return"] = (np.cumprod(data.etf_1_day_return * data.signal + data.etf_2_day_return * (1-data.signal).values + 1) *100)
# 绘制曲线图
_ = plt.figure(figsize=(15, 6))
plt.xlabel('Time')
plt.ylabel('Return')
_ = plt.plot(data["etf_1_return"].index,data["etf_1_return"].values)
_ = plt.plot(data["etf_2_return"].index,data["etf_2_return"].values)
_ = plt.plot(data["signal_return"].index,data["signal_return"].values)
_ = plt.legend(['159967_return', '512890_return', "signal_return"])
ax = plt.gca()
ax.xaxis.set_major_locator(ticker.MultipleLocator(250))
# 计算策略表现指标
result = {}
for i in ['etf_1_return', 'etf_2_return', "signal_return"]:
result[i] = []
for j in ["avg_return", "volatility", "sharpe", "max_drawdown", "win_rate"]:
exec( f"r = qs.stats.{j}(data[i])")
result[i].append(r)
result = pd.DataFrame(result, index=["avg_return", "volatility", "sharpe", "max_drawdown", "win_rate"])
print(result)
回测结果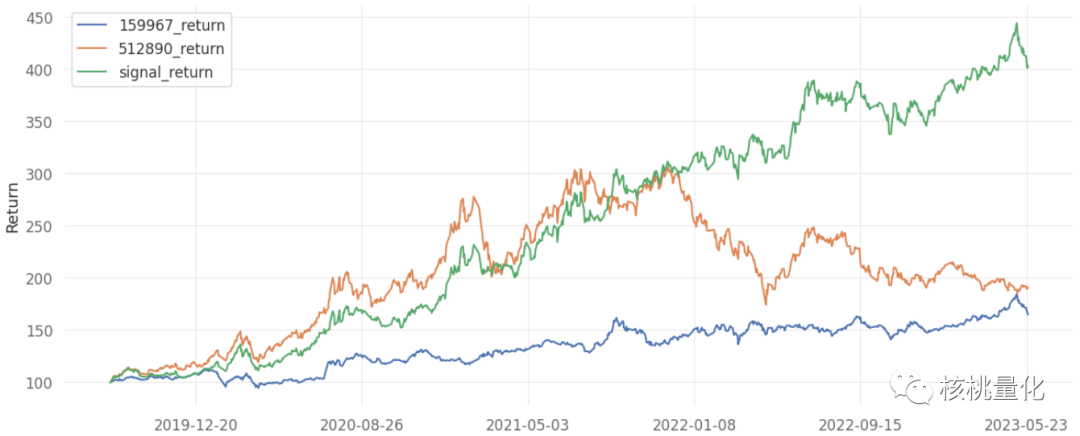
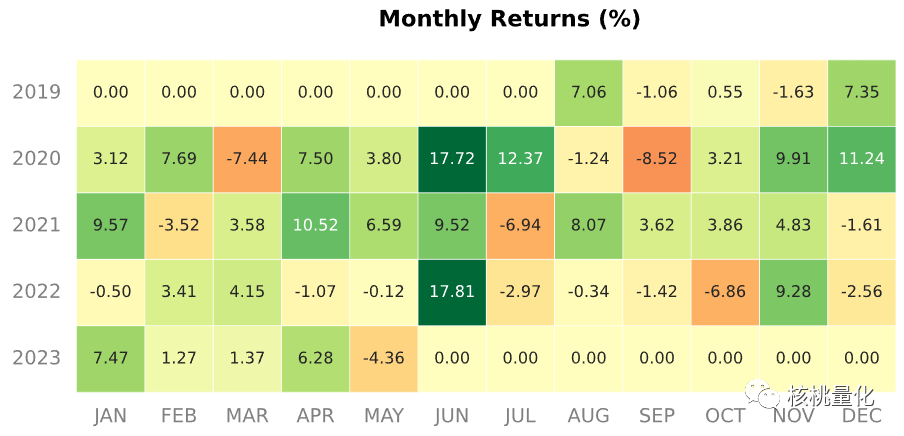
这个策略在整个回测过程中累计调仓60次,年均调仓次数16次。策略的累计回报率高达305%,夏普比率为1.64,年化回报率高达44%,这表明该策略在过去的时间内表现非常出色,远远超过了单独持有红利低波ETF或创成长ETF所能带来的收益。
需要注意的是,上述策略的回测过程未计算调仓手续费和滑点对策略收益产生的影响。且过去的表现并不能保证未来的表现,市场风险和不确定性永远存在。
注 | 本文仅为知识分享,不构成任何投资理财建议。
发布者:股市刺客,转载请注明出处:https://www.95sca.cn/archives/110973
站内所有文章皆来自网络转载或读者投稿,请勿用于商业用途。如有侵权、不妥之处,请联系站长并出示版权证明以便删除。敬请谅解!






