量化投资中的”确定错误”和”模糊正确”

一本文简介

在量化投资中存在两种不同的预测风格，即“确定错误”和“模糊正确”。在处理金融数据时，传统的分类和回归方法可能会出现一些缺陷，因此有序回归被提出作为一种解决方案。有序回归能够处理有序的响应变量、探测响应变量中的阈值效应以及捕捉非线性关系等优势。在实验中，使用有序回归损失函数可以提升模型Rank IC、多空收益、年化超额收益和信息比率，证明了这种方法的有效性。同时也发现将有序回归损失函数与权重均方误差损失函数结合使用可以进一步提高模型效果。

本文只是初步探索了”确定错误”和”模糊正确”的概念。虽然在理论上我们通常会认为模型的精度和投资收益之间应该存在正相关关系，但是实际上，由于金融市场的复杂性和不确定性，精度更高的预测模型并不总是能够带来更好的投资收益。相反，过分追求模型的精度可能会导致过拟合、数据泄露等问题，从而影响后期策略的效果。因此，在金融领域的预测工作中，我们需要将模型精度与实际投资情况相结合，并且要注意选择适当的评价指标和验证方法，以确保我们的预测模型具有实用性和稳健性。

二背景知识

“确定错误”和“模糊正确”

在量化投资中，通常存在“确定错误”和“模糊正确”两种不同的预测风格。

“确定错误”指的是一种追求高精确度的预测风格。这种风格通常会试图以最小化平均误差或最大化预测准确度为目标，其核心思想是通过建立尽可能准确的数学模型，来实现对金融市场的精确预测。然而，在实际应用中，“确定错误”的风格往往会忽略掉市场的不确定性和时变性，从而导致决策失误和风险增加。
相反，“模糊正确”则是一种更加注重适应性和鲁棒性的预测风格。它强调了在金融市场不确定性和时变性的背景下，应该寻求那些可能是正确的，但不一定非常精确的预测方法。这种风格通常采用基于统计学、机器学习等方法的模型，并通过将不确定性和模糊性考虑到模型中，来达到更好的预测能力和风险控制能力。

为什么要追求模糊正确

在选股场景中，由于金融数据的不确定性和时变性，传统的分类和回归方法可能会出现一些缺陷。例如，分类问题将预测目标离散化，从而损失了原始数据中的顺序和距离信息；而回归问题虽然能够更精确地拟合目标值，但是在金融数据的背景下，它往往对异常值比较敏感，有时出现“精确的错误”反而不如“模糊的正确”。因此，我们需要根据具体情况选择适合的方法来处理预测问题，并且需要注意这些方法的局限性。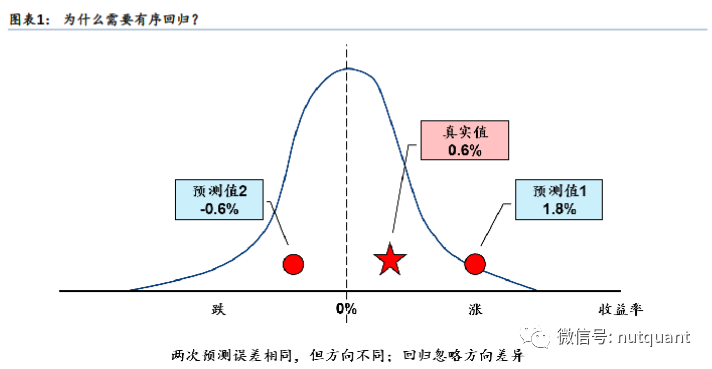

基于上述讨论，我们可以使用有序回归来预测股票收益率，并考虑投资者的风险偏好和需求。例如，我们可以将有序回归模型用于建立一个评估股票收益和风险的指标，帮助投资者进行选股和决策。在使用有序回归模型时，我们需要根据具体情况选择合适的响应变量和预测变量，以获得更准确和实用的预测结果。在这种情况下，有序回归可以作为一种解决方案。

有序回归

有序回归是一种统计学方法，它可以用于处理一个有序的响应变量和多个预测变量之间的关系。与传统的线性回归模型不同，有序回归模型能够考虑响应变量的顺序信息，因此在某些情况下具有优势。以下是有序回归的优势：

能够处理有序的响应变量：有序回归能够很好地处理有序的响应变量，例如对消费者对产品的偏好进行建模时，有序回归模型可以更好地反映产品质量或品牌知名度等因素对消费者购买决策的影响。
能够探测响应变量中的阈值效应：有序回归模型可以识别响应变量中的阈值效应，这在许多实际问题中非常重要。例如，在医疗领域中，研究人员可能需要识别患者生命体征的某个阈值值来预测疾病发展的风险。
能够捕捉非线性关系：有序回归模型还可以用于捕捉非线性关系。例如，如果预测变量与响应变量之间的关系是非线性的，则传统的线性回归模型可能会受到限制，而有序回归模型则可以更好地反映这种关系。

在多分类问题中，我们通常使用交叉熵损失函数来训练模型。这种损失函数主要用于衡量模型输出的预测分布与真实标签之间的差异。然而，在有序回归问题中，我们需要考虑目标变量的顺序信息，并且需要将其划分为若干个有序类别。在这种情况下，交叉熵损失函数就不再适用了。为了解决这个问题，我们可以将传统的交叉熵损失函数改造成一种能够适应有序回归的损失函数。具体来说，我们可以使用 Cumulative Link Model (CLM) 的损失函数来代替传统的交叉熵损失函数。

CLM 是一种基于比例风险模型的有序回归方法，它可以考虑响应变量的顺序信息，并且能够处理多个预测变量。在 CLM 中，我们将响应变量表示成一个有序分类变量，并且假设每个类别之间存在一个阈值点。然后，我们使用最大化 CLM 的似然函数来训练模型，得到能够描述响应变量与预测变量之间关系的模型。在实际预测时，我们可以使用该模型来根据给定的预测变量值，推断出响应变量的期望值或概率分布，从而进行预测。

这个损失函数的核心思想是最大化每个分类阈值处的对数似然，同时保留了响应变量的顺序信息，并且能够处理多个预测变量。相比于传统的交叉熵损失函数，它更加注重对实际投资含义的考虑，并追求“模糊的正确”，将分类和回归的特点结合起来，以兼顾实际投资含义，并追求更加准确和实用的。

三实验总结

参考文献[1]中的工作在周频中证500 指增模型基础上，将加权mse（wmse）损失函数改为不同形式的有序回归损失函数，测试有序回归效果提升。

实验结果显示有序回归损失函数可以提升模型Rank IC、多空收益、年化超额收益和信息比率。同时测试集成有序回归损失函数和wmse损失函数，可以获得更好的效果。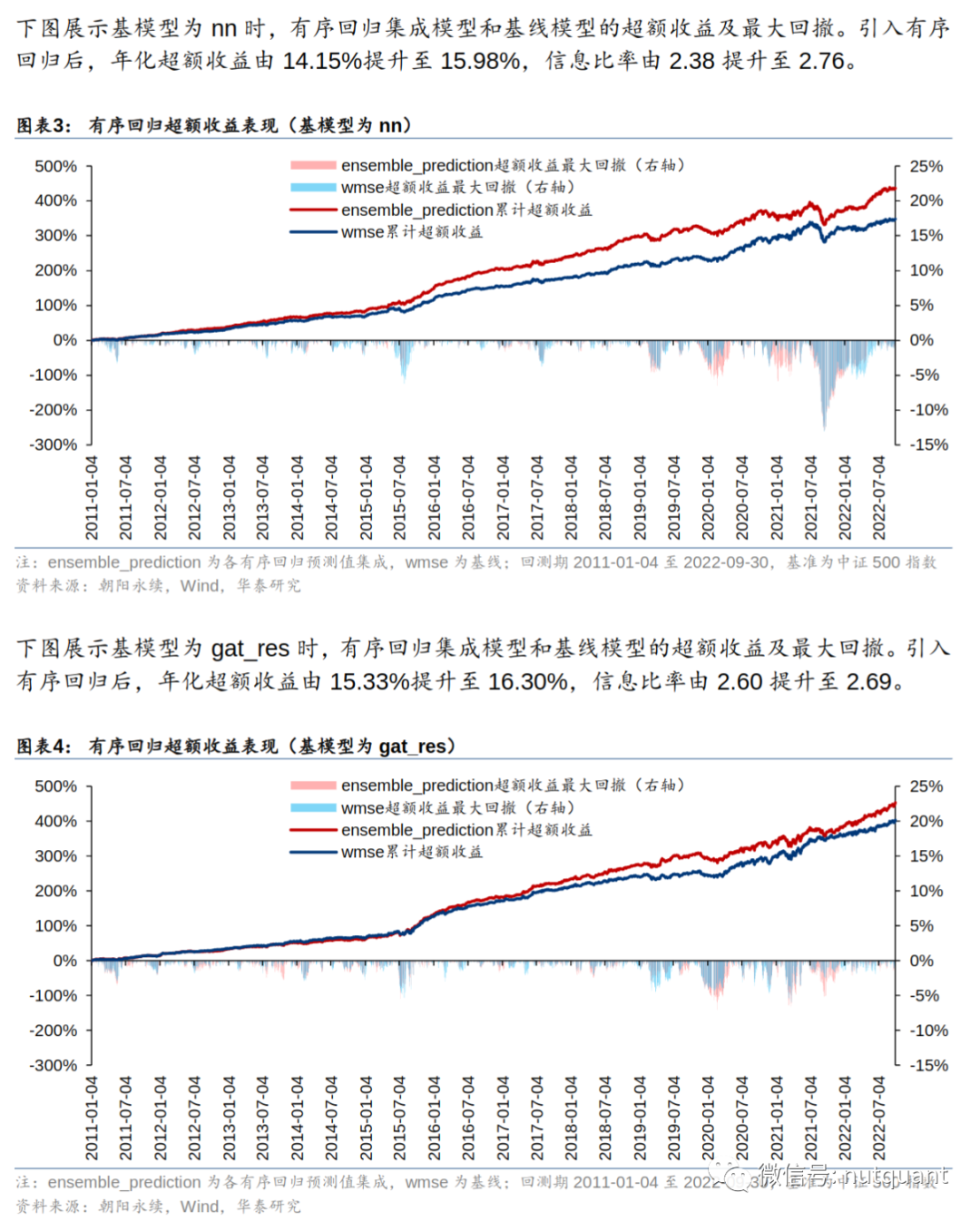

四总结展望

综上所述，我们可以采用有序回归方法来处理金融数据中的预测问题。这种方法能够考虑金融市场的不确定性和时变性，并且能够处理有序的响应变量、探测响应变量中的阈值效应以及捕捉非线性关系等优势。在实验中，有序回归损失函数可以提升模型的表现，证明了它的有效性。未来的工作可以进一步研究如何在不同的金融数据背景下选择合适的预测方法，并且开发更加灵活和高效的有序回归模型。同时，需要注意有序回归模型的局限性，以及在实际应用中需要遵循的投资原则和风险管理策略。

参考文献：
[1] 量化如何追求模糊的正确：有序回归
[2] 维基百科-有序回归
[3] Moving window regression: a novel approach to ordinal regression
[4] THOR: Threshold-Based Ranking Loss for Ordinal Regression