[量化]金融时间序列平滑处理的常见方法和代码实现

代码 

https://github.com/nutquant/QuantCode/tree/main/code/6_time_series_data_smoothing

金融市场数据是非常嘈杂的，因为它受到许多不同的因素影响，例如政治、经济和社会事件等。这些因素可能导致价格波动和不确定性，使得数据分析变得更加困难。

对金融市场数据进行平滑处理可以减少噪音、揭示趋势和降低风险，从而帮助交易员和投资者做出更好的决策，获得更好的回报。平滑后的时间序列数据可以用来：

1. 发现趋势和方向 – 这对于货币、股票、债券或其他金融产品至关重要。长期趋势可以揭示出潜在的大机会，而短期趋势则可以用来掌握时机；
2. 制定策略 – 使用平滑技术，如移动平均线交叉，可以帮助确定何时买入或卖出。这可以让交易员和投资者更有效地管理他们的投资组合，从而获得更好的回报；
3. 为机器学习模型做好准备 – 平滑处理可以大大减少噪音和异常值的影响，从而使机器学习模型更具预测性和可靠性。

下面分享三种常见的金融数据平滑方法。

方法一：移动平均线平滑（不推荐）

移动平均线（Moving Average，简称MA）是最简单的金融数据平滑方法，它通过计算一段时间内的数据的算术平均数来消除价格波动的噪声，使数据变化的趋势更加清晰。移动平均线平滑方法可以分为简单移动平均线和加权移动平均线两种。

• 简单移动平均线是最基本的移动平均线形式，它的计算公式为：SMA = (P1 + P2 + … + Pn) / n 。其中，P1到Pn表示选定的一段时间内的收盘价（或其他指标），n表示选定时间段的长度。简单移动平均线的优点是计算简单、直观，缺点是对较短期的价格波动反应不够灵敏。
• 加权移动平均线是在简单移动平均线的基础上引入加权系数，使得近期的数据对平均值的贡献更大，从而更加灵敏地反映出价格变化的趋势。加权移动平均线的计算公式为：WMA = (w1 * P1 + w2 * P2 + … + wn * Pn) / (w1 + w2 + … + wn) 。其中，P1到Pn表示选定的一段时间内的收盘价（或其他指标），w1到wn表示加权系数，通常采用线性或指数加权方法进行计算。

移动平均线平滑方法可以应用于各种金融数据，如股票价格、股票成交量、利率等。在实际应用中，需要根据数据的特点和所需的平滑效果选择合适的时间窗口和加权方式。下图展示了一个移动平均线随时间窗口增加逐渐变平缓的过程：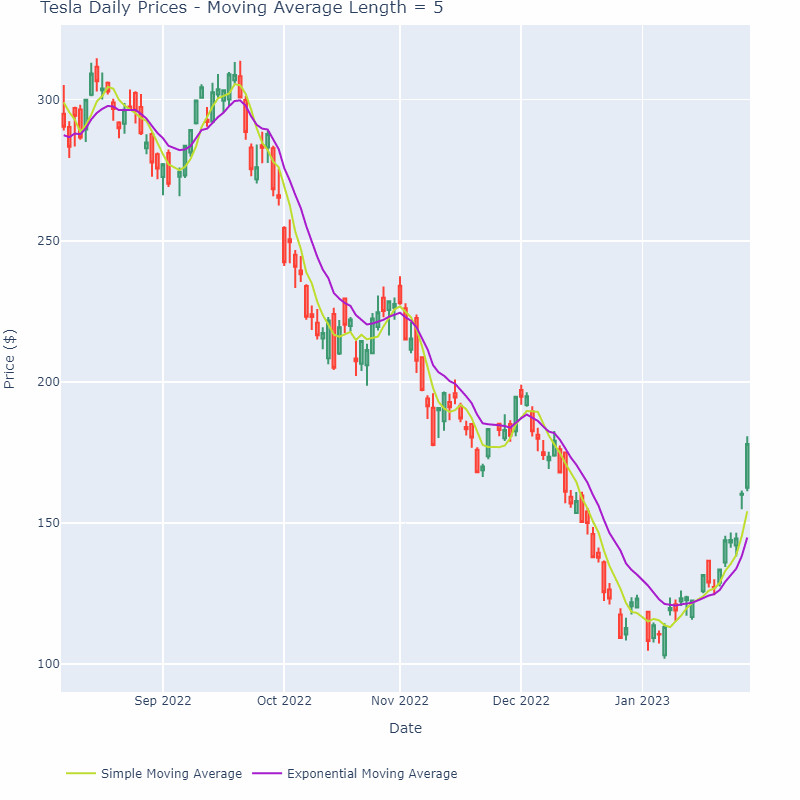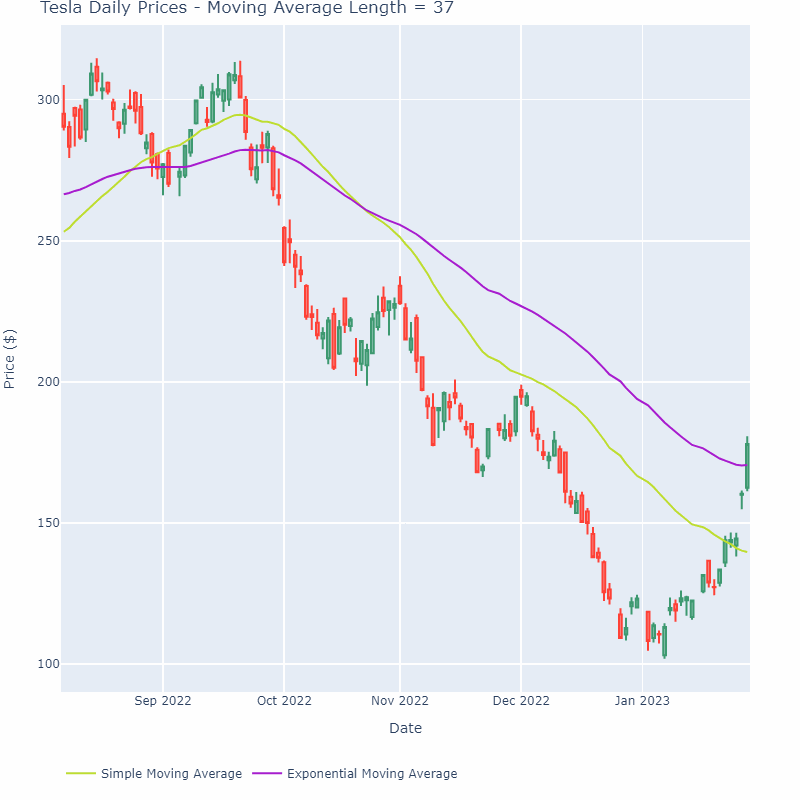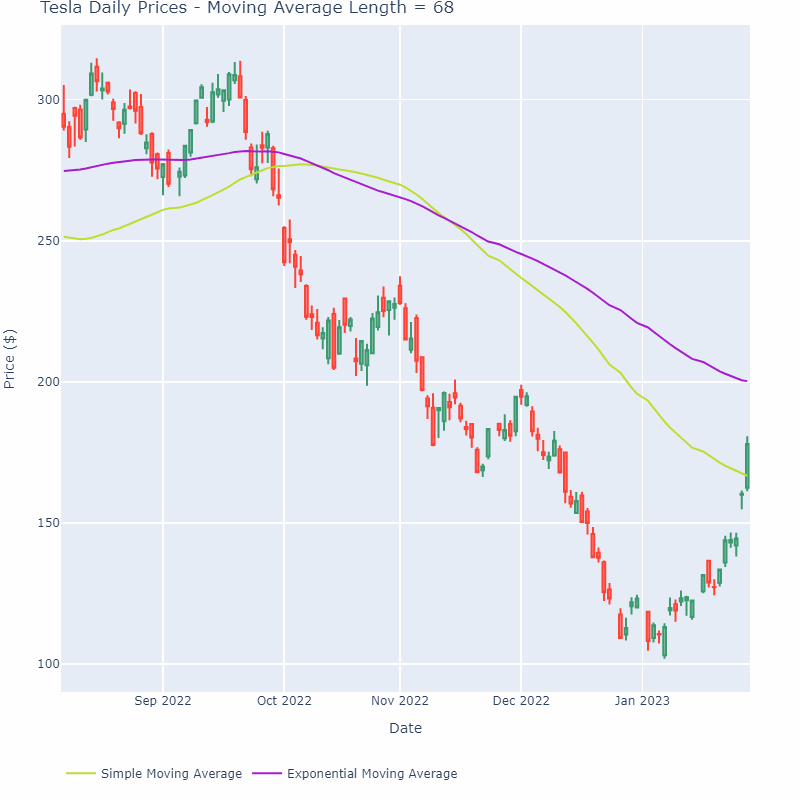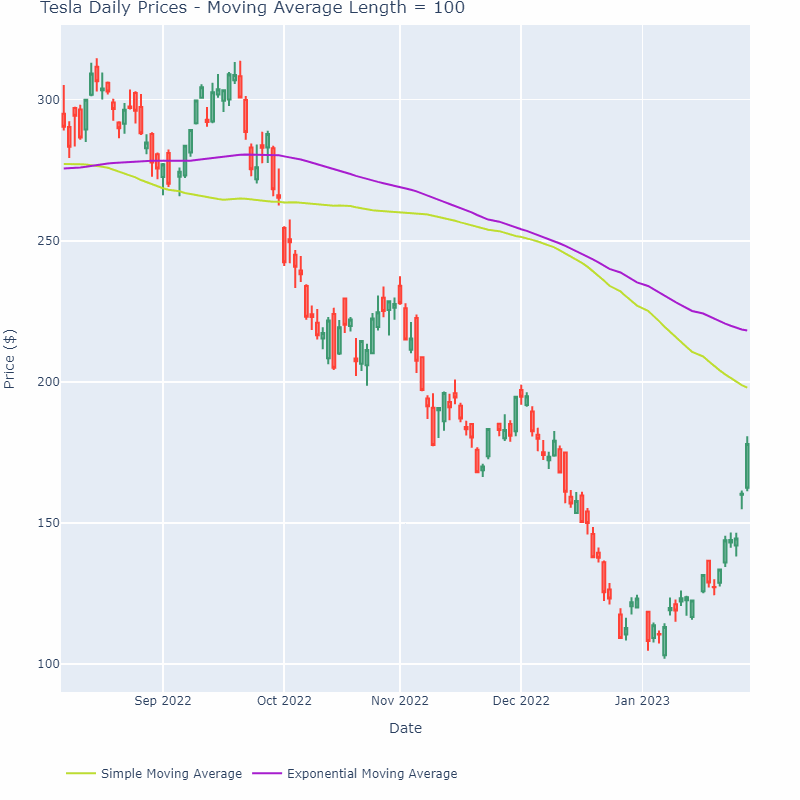

需要注意的是，移动平均线的变化往往滞后于数据。主要原因是它只包含过去一段时间内的数据，而没有考虑未来数据对当前价格趋势的影响。这使得移动平均线成为一种滞后指标，无法预测未来价格的走势。为了解决这个问题，可以使用加权移动平均线或指数移动平均线等方法，赋予最近的数据更大的权重，以更准确地反映当前价格趋势。然而，当数据分布很大或存在双峰分布等异常情况时，平均值可能不是合适的度量，因为它无法反映出数据分布的真实特征。

代码实现：

# 移动平均线平滑
import pandas as pd

def ma_smooth(data, window_length, center=True):
    if isinstance(data, pd.Series):
        smooth = data.rolling(window_length, center=center).mean()
    else:
        data = pd.Series(data)
        smooth = data.rolling(window_length, center=center).mean().values

return smooth

方法二：Savitzky-Golay 滤波器平滑

Savitzky-Golay 滤波器是一种数字信号处理中的平滑滤波器，它在许多领域中都得到广泛应用，包括时间序列和图像处理。该滤波器使用基本思想是对原始数据进行多项式拟合，从而估计平滑后的数据，并在拟合过程中去除噪声和异常值。相比于传统平均滤波器，Savitzky-Golay 滤波器更适用于非线性信号和不同窗口大小下的平滑滤波。
在使用Savitzky-Golay 滤波器进行平滑滤波时，窗口大小和多项式阶数是两个重要参数。简单来说，窗口大小就是进行多项式拟合的数据量，窗口大小越大，数据越平滑。多项式阶数决定曲线的复杂度，阶数越大，曲线形状就越复杂。建议在选择多项式阶数时使用较低的阶数以避免出现问题（对于绝大部分项目，5阶多项式已经足够），并且选择奇数的窗口大小以保持数据对称性。

如下图所示，紫色线是在每个窗口区域内进行多项式拟合的结果。可以看到，随着窗口大小的增加，曲线变得更加平滑，但对于过大的窗口大小，可能会导致滞后效应。因此，在选择窗口大小时，需要权衡平滑程度和滞后效应。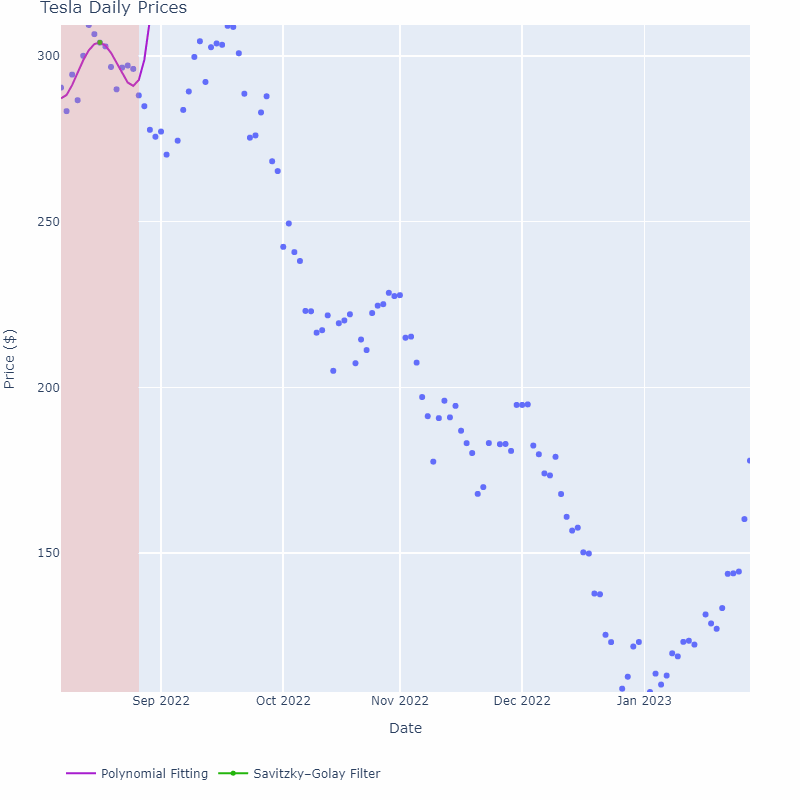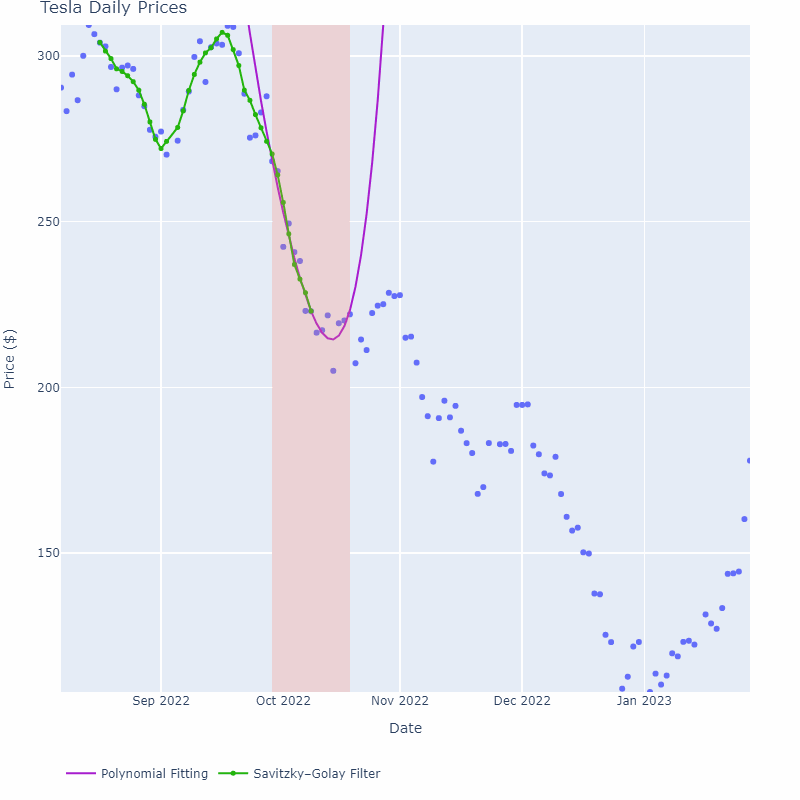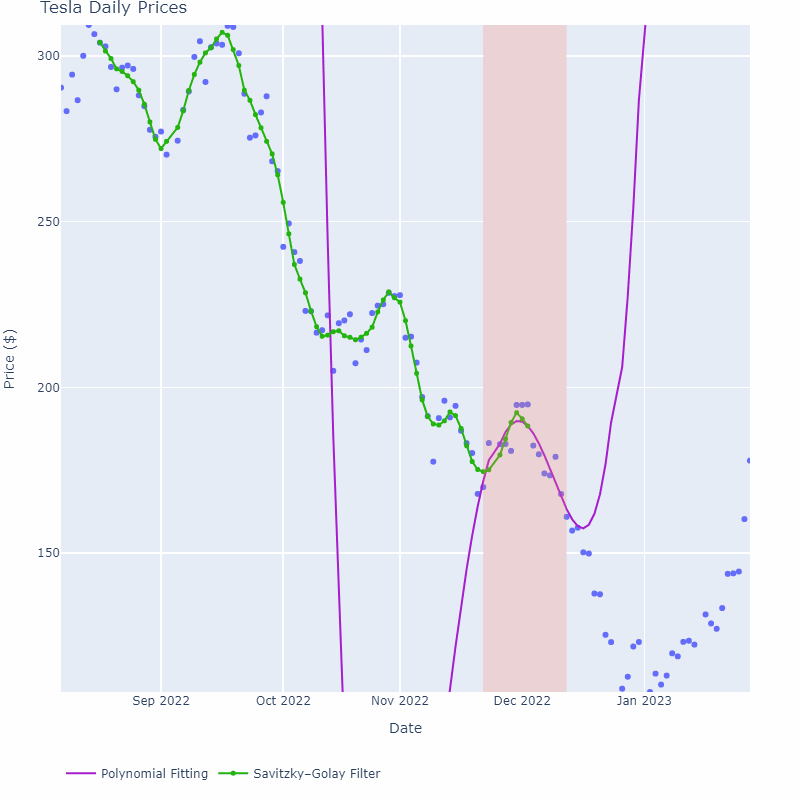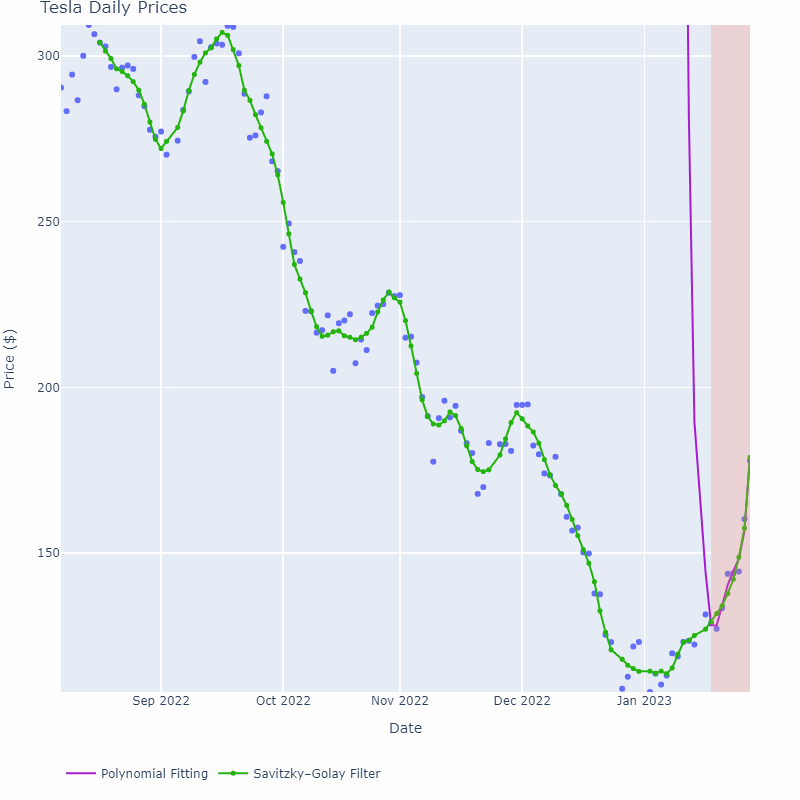

# Savitzky-Golay 滤波器平滑
import pandas as pd
from scipy.signal import savgol_filter

def savgol_filter_smooth(data, window_length, polyorder=5):
  if isinstance(data, pd.Series):
    smooth = savgol_filter(data, window_length = window_length, polyorder = polyorder)
    smooth = pd.Series(smooth, index=data.index)
  else:
    smooth = savgol_filter(data, window_length = window_length, polyorder = polyorder)
  
  return smooth

方法三：偏微分方程平滑(推荐)

使用偏微分方程（Partial Differential Equations，PDEs）来平滑数据是一种常见的方法。偏微分方程有许多种类型，但其中最常用的就是热传导方程和Perona-Malik PDE。它们的基本思想是通过计算数据点之间的差异来确定数据点的变化速率，并根据这些速率来调整数据以获得更平滑的曲线。
偏微分方程来平滑数据是一种非常有用的方法，可以帮助我们去除噪声和异常值，同时保留数据原始的趋势特征。与其他平滑滤波技术相比，偏微分方程方法可以更好地处理非线性信号，同时也具有更高的精度和灵活性。下面是一个简单的动画演示，展示了如何使用偏微分方程来平滑数据。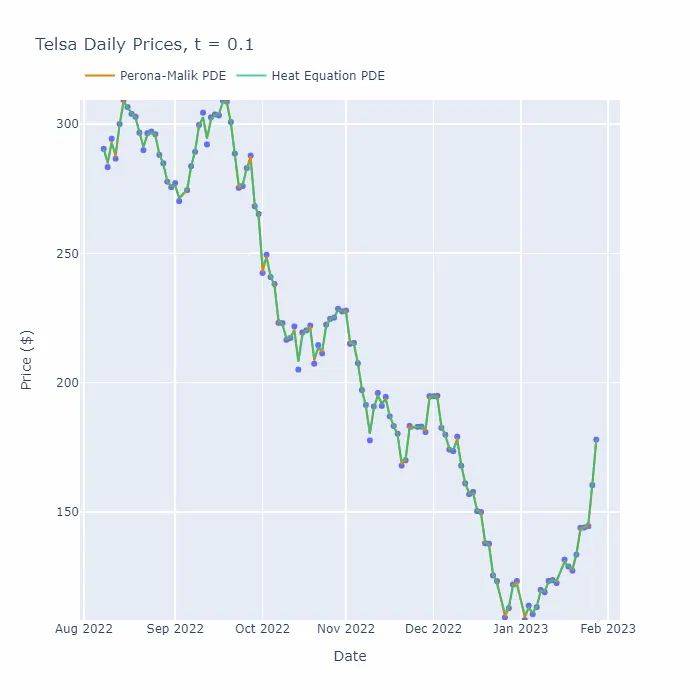

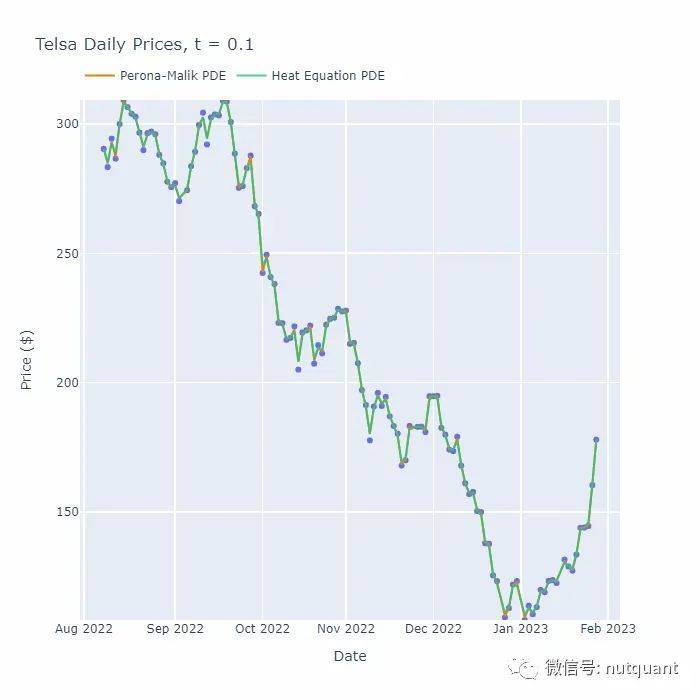
在使用偏微分方程进行平滑处理时，需要注意选择合适的参数来达到最佳效果。例如，在使用热传导方程时，需要选择合适的扩散系数和时间步长。类似地，在使用Perona-Malik PDE时，需要选择合适的阈值参数和时间步长。为了确保平滑质量，还需要在迭代过程中监视误差和收敛速度。使用偏微分方程进行平滑包含以下的优点:

• 完全控制端点：通过使用这种方法，我们可以完全控制平滑曲线的端点，保持它们固定，从而避免它们移动。与其他平滑方法相比，这种方法提供了更高的控制水平，没有必要在平滑后进行人为调整。
• 高计算效率：使用Numba等工具时，这种方法可以快速运行。这使得它能够处理大量数据，并提高了计算效率。与其他平滑方法相比，这种方法的速度更快。

代码实现

# 偏微分方程平滑
import numpy as np
import pandas as pd
from copy import deepcopy

def get_diff_mat(n: int):
    Dx = (
        np.diag(np.ones(n-1), 1) 
        - np.diag(np.ones(n-1), -1)
    )/2
    
    Dxx = (
        np.diag(np.ones(n-1), 1)
        - 2*np.diag(np.ones(n), 0)
        + np.diag(np.ones(n-1), -1)
    )
    
    return Dx[1:-1, :], Dxx[1:-1, :]
    
def _heat_smooth(p: np.array,
                 k: float = 0.05,
                 t_end: float = 5.0):

    _, Dxx = get_diff_mat(p.shape[0])
    U = deepcopy(p)
    t = 0
    
    while t < t_end:
        U = np.hstack((
            np.array([p[0]]),
            U[1:-1] + k*Dxx@U,
            np.array([p[-1]]),
        ))
        
        t += k
        
    return U

def heat_smooth(data, k=0.05, t_end=1, window=21):
  if isinstance(data, pd.Series):
    smooth = data.values.copy()
    for i in range(0, len(smooth), window):
        smooth[i:i+window] = _heat_smooth(smooth[i:i+window], k, t_end)
    smooth = pd.Series(smooth, index=data.index)
  else:
    smooth = data.copy()
    for i in range(0, len(smooth), window):
        smooth[i:i+window] = _heat_smooth(smooth[i:i+window], k, t_end)
    smooth = _heat_smooth(data, k, t_end)
  
  return smooth

需要注意的是，平滑效果较好的方法往往是使用了居中窗口的方法，即在平滑过程中即使用了过去数据，又使用了未来数据。这种方式会导致未来信息的泄露，因为在实际交易中，我们无法事先得知未来的价格变化，只能根据过去和当前的数据来做出决策。所以使用未来数据进行平滑的方法只用于分析数据，发现趋势，不能作为机器学习的标签进行使用。

参考：
[1] A Surprising Way To Smoothen A Time Series — Solving The Heat Equation!
[2] 3 Easy Ways to Smoothen Time Series Data For Finance
[3]  You’re Using the Wrong Average in Your Financial Analysis