小概率的事情为什么会发生

我们做一个理想的假设。按照詹姆斯·杰恩斯的说法， 空气里一共有10的44次方个分子，而每个人呼吸会用到10的22次方个分子。现在假如地球的空气一直在自我循环并且充分融合，那么我吸一口气恰好吸到一个柏拉图吸过的分子的概率是：

这几乎是一个不可能事件。但问题在于我不一定只有一次机会，从概率上来说，我实际上也有10的22次方次机会吸到这个分子，于是我至少吸到过一个柏拉图吸过的分子的概率就变成了：

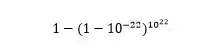
这个值计算下来大约是0.64左右。当然这里我们还需要假设，每次呼吸事件是独立的，因为如果我们是一个接一个吸分子的话，这次吸入分子减少了分子的总数，这样成功的概率就会变化。所以这个概率比较理想化，但是至少能帮助初中时候的我理解，为什么我有机会吸到柏拉图吸过的分子。尽管我只想说，柏拉图你好大的口气。后来有一个数学家专门在The American Mathematical Monthly写过文章说这个问题的严谨解法，不过我没有看懂。

如今很多问题都会用概率来表达，尤其是安全性之类的问题，比如飞机就会用每一百万次飞行的事故率来强调自己很安全，而数据可能是每百万次会有零点几个人丧命，而实际上，对于我们大多数人来说，小概率事件背后的分母差异其实没有太大的理想，一亿分之一和一千万分之一的概率值从数字上看已经有了量级的差异，但是对于我们的理解来说，如果我分别用这两个概率来形容我娶到林志玲和娶到高圆圆的可能性，却又是没有差异的。这样的形容词只是表达我不死心的态度，而非精确的衡量单位。

实际上大部分真正的概率，即便听上去小得不可思议，但是如果基于其来源的背景视角，就又并非那么神奇了。曾经有一个英国数学家叫李特尔伍德（John Edensor Littlewood），他说，奇迹就是一件重大意义的事情发生了，而他发生的概率只有百万分之一。这句话听上去没毛病，但是他告诉我们每个人大约一个月就会发生一次奇迹，这就是传说中的李特尔伍德奇迹法则。实际上如果仅仅是基于概率来说，奇迹在我们人生中出现的频率非常之高，比如抛硬币20次，得到了一个正反面的组合，这个组合出现的概率是：

结果差不多就是百万分之一。这种想法简直是对奇迹这个词的亵渎，你一定是这么想的。但是百万分之一真的不是一个很夸张的概率事件，举一个简单的例子，假如在中国你只有百万分之一的机会成为一名魔法师，那么实际上已经有1000多个中国人成功拿起了魔杖，按照哈利波特里的出场人物数量，这已经足够组建魔法部了。

那么我们到底如何衡量不可能事件呢？这里就必须提到一个人了，他叫泊松（Simeon-Denis Poisson）。以前有个著名的题目，一个国际象棋的棋盘有64格，现在给你64粒米，任意摆放到其中的格子上，那么a1格上一粒米都没有的概率是多大？

用刚刚算气体分子的公式算一下，结果是：

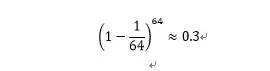
这是一次尝试，如果我们尝试一百万次的话结果会是怎么样呢？实际上就是把64次方替换成100万就好，此时我们的概率值不会偏离0.3太多，大概会接近0.3679，恰好等于一个神奇的数字e^-1，这就引出了一个小概率事件定律：如果一个事情之前只发生过一次，以后发生的概率很难预测，那么这件事情以后不发生的概率就是e^-1，差不多37%。刚才柏拉图那个问题的结果实际上也非常接近，我们没有吸到柏拉图吸过的分子的概率恰好也是36%多。这真是一个非常神秘而又奇怪的定律。实际上这就是泊松分布的基础，大学学过又忘掉的人可以去面壁了。

任何事情只要重复的次数够多，再小概率的事情都不意味着不会发生，所谓有志者事竟成就是这么个道理。就好像我们觉得随机性与规律性是一对矛盾，但是当一个事件以随机的形式出现很多次之后，自然就出现了一条冥冥中存在的规律，我们惊叹于奇迹的小概率，事实上寻常同样也来得不易。