为了在实际的贸易中更有竞争力，很多企业开始了一些含权贸易。这些双方协定的期权往往包含一些特殊条件，例如分批执行，含障碍，以及有敲入敲出条件等等。例如当前价格是5700，但是通过含权报价，可以把价格降低至5600，这样对客户会更有吸引力。而在一些特殊的合同条件下，采用传统的BS模型往往很难对这些期权定价，所以我们需要一个更加直观的算法来实现对期权的计算。

蒙特卡洛算法介绍

20世纪40年代，在科学家冯·诺伊曼、斯塔尼斯拉夫·乌拉姆和尼古拉斯·梅特罗波利斯于洛斯阿拉莫斯国家实验室为核武器计划工作时，发明了蒙特卡罗方法。因为乌拉姆的叔叔经常在摩纳哥的蒙特卡洛赌场输钱得名，而蒙特卡罗方法正是以概率为基础的方法。

蒙特卡洛的逻辑就是采用尽可能多的随机生成数，来生成结果，然后从结果的分布倒推出正确结果的分布特征。就像1奇异博士看了未来1400万中可能后选择一个方案一样，我们虽然不能通过时间宝石看到这么多结果，但是可以用计算机模拟出更多的可能性来！

实际运用过程就是

先随机生成尽可能多的价格波动过程，
计算每一个价格过程得到的期权收益，
根据结果倒推出期权的收益特征。

代码实战

欧式期权

欧式期权是最简单的一种期权，通常欧式期权可以使用BS公式直接计算出来，当然我们也可以使用蒙特卡洛过程来计算期权收益。

举例：当前价格为5700，执行价格为5800的欧式看涨期权，还有120日到期，标的日波动率0.0063，无风险收益率为0.

采用bs定价模型得到结果是

from scipy.stats import norm  
from math import log, sqrt, exp  
S = 5700 #当前价格  
K = 5800 #执行价格  
s = 0.0063 #日波动率  
t = 120 #到期日  
r = 0.0 #无风险利率  
def CND(X):  
    return norm.cdf(X)  
def CallOptionPriceBS(S, K, s, t, r):    
    d1 = (log(S / K) + (r + (s ** 2) / 2) * t) / (s * sqrt(t))    
    d2 = d1 - s * sqrt(t)    
    return S * CND(d1) - K * exp(-r * t) * CND(d2)  
CallOptionPriceBS(S,K,s,t,r)
> 结果 np.float64(113.27621835900891)

采用蒙特卡罗方法定价

# 生成模拟价格  
import numpy as np   
def SimulatePrice(P0, std, steps, step_price=1, N=10000):  
    """  
    :param P0:  初始价格  
    :param std:   序列标准差  
    :param steps:   序列步数  
    :return:  
    """    sim_norm_ret = np.random.normal(0, std, (steps, N))  
    sim_price = np.exp(sim_norm_ret.cumsum(0))  
    # # 初始价格1000  
    sim_price = P0 * sim_price  
    sim_price = (sim_price / step_price).round(0) * step_price  
    # 第一行添加初始价格  
    sim_price = np.vstack([P0 * np.ones(N), sim_price])  
    return sim_price  
  
S = 5700 #当前价格  
K = 5800 #执行价格  
s = 0.0063 #日波动率  
t = 120 #到期日  
r = 0.0 #无风险利率  
sim_price = SimulatePrice(S,s,t,1,100000)  
# 持有看涨期权最终的收益  
payoff = np.maximum(sim_price[-1, :] - K, 0)  
payoff.mean()
> 计算结果 np.float64(118.50833) 每次计算结果会不同

需要注意的是蒙特卡罗算法只能逼近结果，而不是精确的最终结果。N越大结果越逼近，但是需要的算力也越大（当然现在算力不值钱）

奇异期权

考虑下面一种备兑期权的报价，假定期货价格和现货价格相同当前白糖价格是5700，我们向下游签订供货合同，在未来120天的观察期内，每天按照要求。

如果期货价格在5600-5800之间，我们按照5650价格供货1吨
如果价格跌破5600，我们按照5600价格供货2吨
如果价格在5800以后，合同终止这样的期权如果采用BS定价方式，计算起来比较绕。但是如果采用蒙特卡洛算法就很简单

def contract(price_array):  
    """  
    :param price_array::return:   
    """  
    strike_price = 5600  
    supply_vol = 0  
    supply_profit = 0  
    for i in range(len(price_array)):  
        p = price_array[i]  
        if p < strike_price:  
            supply_vol += 2   
# 在5650以下的时候，我们的盈利是5650-p 供货2吨  
            supply_profit += (strike_price  - p) * 2     
elif strike_price <= p < 5800:  
            supply_vol += 1   
# 在5650-5800之间的时候，我们的盈利是5650-p 供货1吨  
            supply_profit += strike_price - p   
        else:  
            break  
    return supply_profit, supply_vol  
sim_price = SimulatePrice(S,s,t,1,100000)  
sim_profit = np.zeros(sim_price.shape[1])  
for i in range(sim_price.shape[1]):  
    supply_profit, supply_vol = contract(sim_price[:, i])  
    sim_profit[i] = supply_profit  
print(sim_profit.mean())  
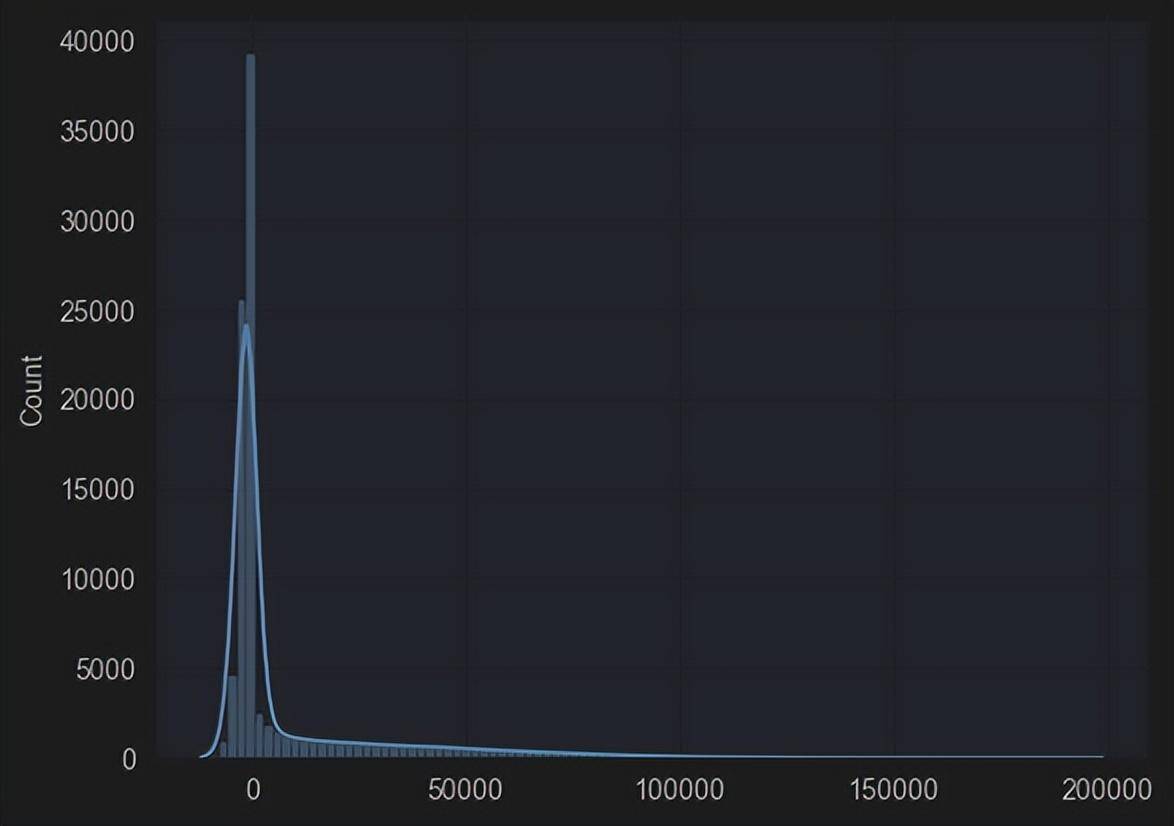
sns.histplot(sim_profit, kde=True, bins=100)
>结果 8885.40254