使用Wasserstein k-means的聚类方法进行市场模式识别

一 本文摘要

时间序列分析在各个领域中都很重要，特别是在金融领域。人们使用时间序列分析来量化过去和当前的经济状况，或者寻找投资机会。聚类算法可以帮助我们在时间序列数据中发现不同的模式。最近有一种称为Wasserstein k-means（Wk-means）的聚类方法被提出，特别适用于一维资产收益数据。本文研究尝试将该方法还扩展到多维时间序列数据，并引入了切片Wasserstein k-means（sWk-means）聚类方法。这些方法在金融领域中有重要的应用，可以帮助我们理解和分析时间序列数据中的模式，特别是在无监督学习的情况下。

二 背景知识

2.1 市场模式

市场模式识别是一种金融分析技术，旨在识别和理解金融市场中的不同模式和趋势。通过对市场数据进行分析，包括价格、交易量和其他相关指标，可以发现市场中的重复模式和趋势，从而提供决策支持和预测未来走势的依据。市场模式识别可以应用于各种金融市场，如股票市场、外汇市场和商品市场。它可以帮助投资者和交易员识别市场中的重要转折点、趋势延续和价格震荡等情况。常用的市场模式包括趋势模式、反转模式和震荡模式。趋势模式指的是市场价格朝着特定方向持续变化的情况，可以是上涨趋势或下跌趋势。反转模式指的是市场价格发生逆转的情况，即从上涨转为下跌或从下跌转为上涨。震荡模式则表示市场价格在一定范围内波动，没有明显的趋势方向。

2.2  聚类算法

聚类算法是一种机器学习的方法，它可以将一组数据对象分成不同的组或簇，使得同一组内的对象彼此相似，而不同组之间的对象差异较大。我们可以将聚类算法想象成给一堆混在一起的物品进行分类的过程。假设我们有一些水果，如苹果、橙子和香蕉，我们想要将它们按照它们的特征分成不同的组，比如将所有苹果放在一组，将所有橙子放在另一组。

聚类算法的工作方式是根据数据对象之间的相似性或距离来进行分组。算法会根据对象之间的相似性将它们聚集在一起，同时尽量使不同组之间的差异最大化。这样一来，我们就可以在不知道具体类别的情况下，发现数据中的模式和结构。

2.3  Wasserstein距离

Wasserstein距离是一种用于度量两个概率分布之间差异的距离度量指标。它也被称为地面距离、Kantorovich-Rubinstein距离或移动距离。与传统的距离度量（如欧氏距离）不同，Wasserstein距离考虑了概率分布之间的结构和形状差异。我们可以将概率分布看作是一定数量的质量或物质在不同位置上的分布。Wasserstein距离通过计算将一个分布转化为另一个分布所需的最小代价，来衡量这两个分布之间的差异。这个代价可以被理解为将一个分布中的质量重新分配到另一个分布上的最小成本。

直观地说，Wasserstein距离可以看作是一个分布转化为另一个分布所需的最小运输成本。这种运输成本可以被解释为将一个分布中的“质量”从一个位置移动到另一个位置的成本。因此，Wasserstein距离可以捕捉到两个分布之间的形状差异和质量重新分配的程度

三 本文工作

3.1 Wasserstein k-means聚类算法

当我们处理多维时间序列数据时，我们需要一种有效的方法来将这些数据进行聚类。其中一种方法是使用Wasserstein k-means聚类算法，它是一种基于Wasserstein距离的无监督学习算法。首先，我们定义了数据流和经验分布的概念。数据流是一系列数据点的集合，例如金融领域中的价格路径。经验分布是对数据流的统计描述，它告诉我们每个数据点出现的概率。接下来，我们引入了Wasserstein距离的概念。Wasserstein距离是一种衡量两个经验分布之间差异的度量。它考虑了两个分布之间的最佳匹配方式，以及将一个分布转换为另一个分布所需的成本。通过计算Wasserstein距离，我们可以衡量数据流之间的相似性或差异性。

为了进行聚类，我们使用了Wasserstein k-means算法。这个算法首先定义了点之间的距离，即Wasserstein距离。然后，它通过计算数据点的平均值来找到聚类的中心点，这个平均值被称为Wasserstein质心。然后，算法将数据点分配到离其最近的质心，形成聚类。

伪代码实现：

然而，对于高维数据，计算完整的多维Wasserstein质心可能是非常耗时的。为了解决这个问题，我们引入了切片Wasserstein距离的概念，它是多维Wasserstein距离的一个近似。通过在算法中使用固定的投影方向，我们可以避免计算完整的多维Wasserstein质心，这使得算法更容易实现和计算效率更高。

3.2 sWk-means聚类算法

sWk-means方法是一种用于聚类数据的算法，特别适用于处理时间序列数据。它使用了Wasserstein距离和切片Wasserstein距离的概念。下面是整个算法的流程描述：

1. 首先，我们有一组时间序列数据，例如金融市场的价格路径。为了进行聚类，我们首先对数据进行转换，计算数据的收益率，并对其进行标准化。然后，我们对这些转换后的数据进行另一个转换，得到一组经验分布，描述了数据的统计特征。
2. 接下来，我们选择一组固定的向量，定义了一个在多维空间中的网格。然后，我们将每个经验分布投影到这个网格上，得到一组投影分布。这些投影分布是经验分布在不同方向上的投影。
3. 然后，我们使用k-means算法来进行聚类。算法首先随机选择一些经验分布作为初始的聚类中心。然后，对于每个经验分布，我们计算它与每个聚类中心之间的切片Wasserstein距离，并将它分配到距离最近的聚类中心所在的聚类中。
4. 接下来，我们更新每个聚类中心，将它们设定为属于该聚类的投影分布的切片Wasserstein重心。这个重心是投影分布的平均值。
5. 我们继续迭代这个过程，直到聚类中心不再移动或者移动的变化很小为止，这就表示算法已经收敛。

伪代码实现：

四 实验结果

实验部分通过对合成的二维和三维时间序列数据进行实验，我们展示了sWk-means算法在这些数据上的良好表现。具体而言，该算法能够捕捉到具有相同均值和协方差的不同模式之间微妙差异。这意味着算法能够有效地区分并聚类这些时间序列数据。

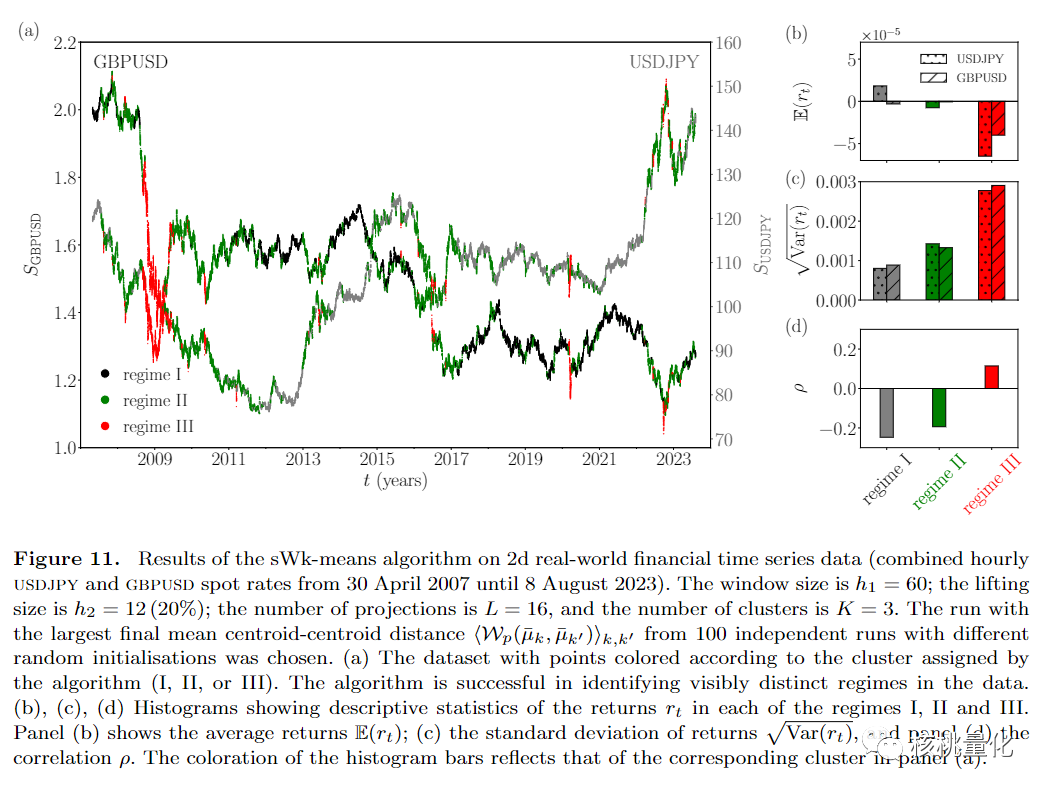
此外，实验部分还将sWk-means算法应用于实际的二维金融时间序列数据，具体是使用公开可得的外汇即期汇率数据进行了案例研究。结果表明，该算法能够在这些金融数据中有效地识别出不同的模式，而且这些模式的特征可以通过事后分析，如描述性统计等方法进行更深入的分析。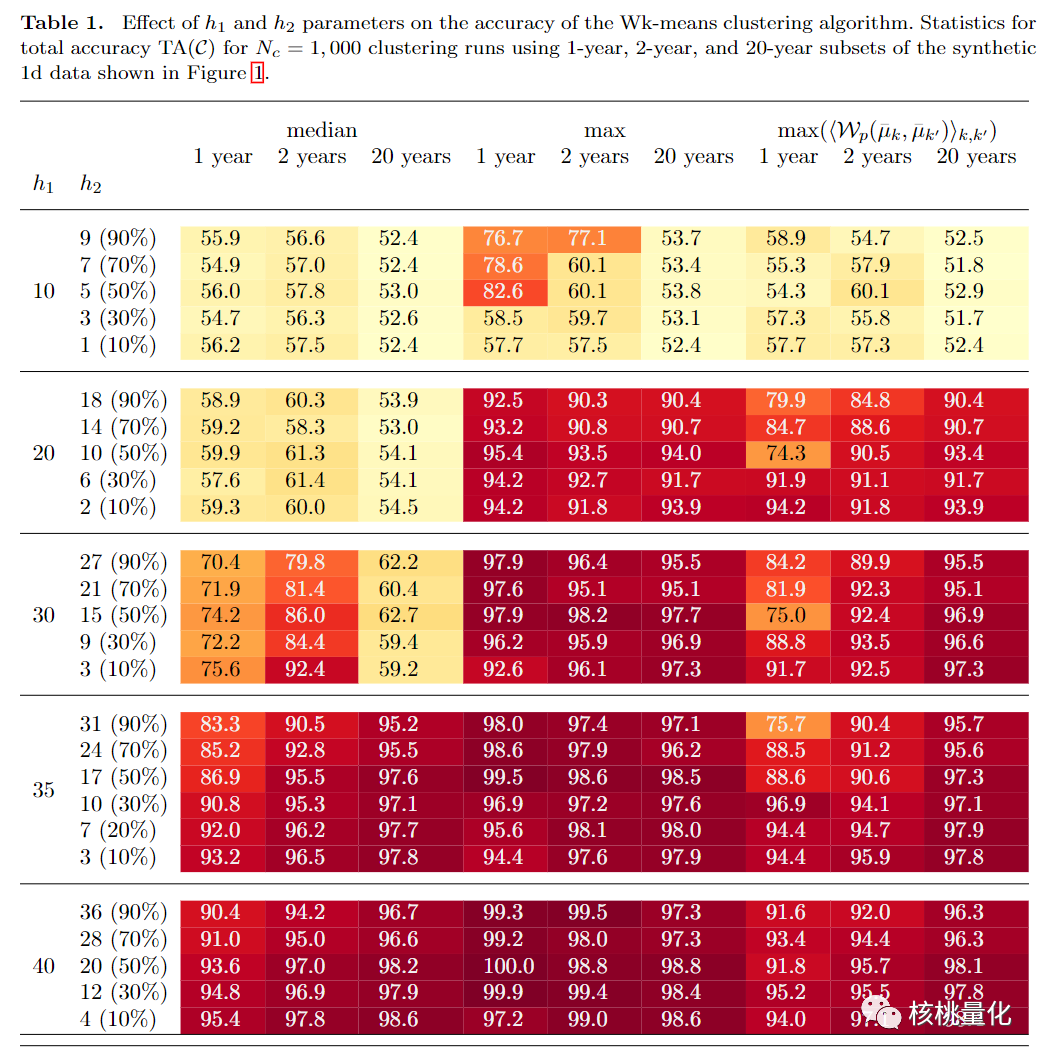

五 总结展望

本文详细研究了Wk-means算法在一维时间序列数据上的行为，并通过扩展算法，即切片Wasserstein k-means（sWk-means）聚类，使其适用于多维时间序列数据。sWk-means算法利用固定投影向量网格简化实现过程并减少计算成本。研究结果显示该算法在二维和三维情况下表现良好，能够捕捉不同模式之间微妙差异的特征。此外，论文讨论了隐马尔可夫模型（HMM）作为sWk-means的替代方法，并发现在某些情况下，HMM也能够识别合成数据中的模式。