|
《Realized semibetas:Disentangling “good” and “bad” downside risks》
https://public.econ.duke.edu/~ap172/BPQ_semibeta_14apr21.pdf
|
| 本文提出了一种新的市场beta分解方法,将传统的市场beta分解为四个semi-beta(semibetas),这些semi-beta基于市场与个别资产回报之间的有符号协方差。研究发现,与市场负回报和资产负回报协方差相关的semi-beta能够显著预测未来更高的回报,而与市场负回报和资产正回报协方差相关的semi-beta则预示着未来更低的回报。文章的结论是,与其与传统的市场beta对赌,不如选择“正确”的semi-beta进行投资。 |
本文最后对上述4种beta做了简单复现,感兴趣的同学可以翻到最后查看。
本章介绍了资本资产定价模型(CAPM)的基本概念,并指出了传统市场beta在解释资产横截面收益变化时的局限性。作者提出,投资者可能更关注损失而非收益,因此风险的度量不应仅仅是总体方差,而应是负面回报的半方差。
尽管CAPM在理论上具有吸引力,但实证研究却反复揭示了其在解释资产回报横截面变化时的不足。一些研究指出,CAPM所估计的风险溢价往往过低,有时甚至微不足道或呈现负相关,这与CAPM的预测相悖。
如下为4张假设的二元分布轮廓图,每个分布都具有标准正态边际分布,并且都隐含了一个CAPM beta值为1,横轴为资产收益率、纵轴为市场收益率。
• Panel A 展示了一个与市场共同正态分布的资产,其正负收益的协方差(N和P)相等,混合符号的半协方差(M+和M-)也相等。在这种情况下,CAPM预测该资产的预期收益与市场一致。
• Panel B 展示了一个在市场下跌时相关性较低,而在市场上涨时相关性较高的资产(βN < βP)。根据semi-beta模型的结果,资产B的年预期超额收益低于资产A,这与投资者特别厌恶下行风险的观点一致。
• Panel C 展示了一个在市场下跌时比市场上涨时更具有正相关的资产(βN > βP),这从均值-半方差的角度来看是不受欢迎的,因为它增加了下行收益的变动性。然而,这种资产的预期收益却比资产A和B要高,这与CAPM的预测相矛盾。
• Panel D 展示了一个在市场下跌时比市场上涨时更具有正相关的资产,但其混合半协方差(βM- > βM+)赋予了它相对于资产C更好的对冲效益,因此预期收益较低。
在这样的背景下,本文作者提出了一种新的市场beta分解方法——semi-beta。这一创新的分解基于市场与个别资产回报之间的有符号协方差,将传统的市场beta细分为四个部分:βN、βP、βM+和βM−。
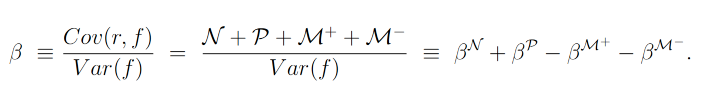
文章中,作者展示了semi-beta与未来回报之间的关系。特别是,与市场负回报和资产负回报协方差相关的βN,以及与市场负回报和资产正回报协方差相关的βM−,被发现能够显著预测未来的回报。这一发现与传统CAPM的线性假设形成了鲜明对比,为投资者提供了更为细腻的风险评估工具。
在金融分析领域,市场beta是一个衡量资产相对于整个市场波动性的指标。传统上,市场beta的计算基于资产回报率与市场回报率之间的协方差,而不考虑回报率的正负符号。然而,这种传统的计算方法可能无法充分捕捉市场下行风险,即所谓的“坏”风险,这在投资者的决策过程中是一个重要的考量因素。
—— semi-beta的创新性定义 ——
本文作者提出了一种新的市场beta的分解方法,将传统的市场beta分解为四个semi-beta,这一创新性定义基于市场与个别资产回报之间的有符号协方差。具体来说,semi-beta的计算公式如下:
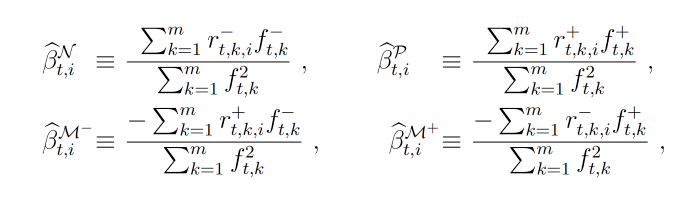

其中,r 表示某个风险资产的回报率,f 表示市场组合的回报率,Cov 表示协方差,Var 表示方差,βN、βP、βM+ 和 βM− 分别对应于市场和资产回报同时为正(P状态)、同时为负(N状态)、市场为正资产为负(M+状态)和市场为负资产为正(M-状态)的semi-beta。
—— semi-beta的数学含义 ——
从数学角度来看,semi-beta的分解提供了一种更为细致的视角来分析资产与市场之间的关系。传统的市场beta只考虑了整体的协方差,而不考虑回报率的正负,这可能导致对风险的评估不够精确。semi-beta的引入,允许我们区分资产在市场上涨和下跌时的不同表现,从而更准确地评估资产的系统性风险。
—— semi-beta在量化投资中的应用 ——
在量化投资领域,semi-beta的概念可以被用来构建更为精细化的风险模型和投资策略。例如,通过识别具有较高βN的资产,投资者可以寻找那些在市场下跌时表现出相对较小负回报的投资机会。相反,通过避免或做空具有较高βM−的资产,投资者可以减少在市场下跌时的潜在损失。
本文的第三部分深入探讨了作者提出的semi-beta与预期回报之间的横截面联系,为我们提供了一个全新的视角来洞察资产定价的复杂性。
作者通过实证分析,展示了semi-beta如何显著预测未来的回报。此处不详细展示文章的统计过程,感兴趣的同学可以自己翻看原文。具体来说:
• βN(与市场负回报和资产负回报协方差相关的semi-beta)预示了未来更高的回报。
• βM−(与市场负回报和资产正回报协方差相关的semi-beta)预示了未来更低的回报。
• βP 和 βM+(与市场正回报相关的semi-beta)则没有显示出明显的定价效应。
这些发现挑战了传统的CAPM理论,其中市场beta是预期回报的唯一决定因素。semi-beta的引入提供了一种更为细致的风险度量,允许投资者区分不同市场条件下的资产表现。
—— 数学模型与实证方法 ——
作者使用了Fama-MacBeth回归方法来估计semi-beta的风险溢价。这种方法允许作者在每个时间截面上估计风险溢价,然后通过时间序列的平均来得到平均风险溢价的估计值。具体的回归模型可以表示为:
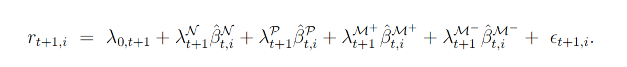
其中,rt+1,i 表示资产 i 在时间 t+1 的回报率 λj,t+1 表示不同semi-beta的风险溢价,β^j,t,i 表示在时间 t 对资产 i 的semi-beta估计值。在实际的投资决策中,投资者往往更加关注资产在市场下跌时的表现,因为这直接关系到资本的保值和风险控制。
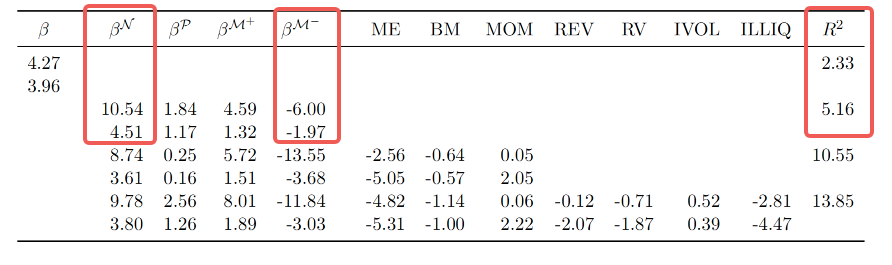
下图是基于1963年1月至2019年12月期间所有CRSP数据库的股票数据,使用每日数据计算得到的每月实现semi-beta进行的Fama-MacBeth回归结果。重要的结论有以下几点:
• 传统CAPM模型的Beta风险溢价为4.27%;βN风险溢价为10.54%且t统计量为4.51呈显著,βM- 风险溢价为-6.00%同样呈显著
• CAPM模型的Beta回归的R²为2.33%,当包括semi-beta时,模型的R²提高到5.16%,表明semi-beta提供了比传统CAPM更多的解释力;当进一步包括其他控制变量时,模型的R²提高到13.85%,同时semi-beta的风险溢价依然显著。
• βN和βM-的风险溢价在统计上显著,而βP和βM+则不显著,这表明市场对负面共同变动的风险给予了更高的溢价。
随着高频数据的日益可用,研究者能够更精确地测量和分析市场行为。本文的第四部分专注于利用高频数据来构建每日semi-beta,旨在捕捉市场波动中的更细微变化。
作者采用15分钟的高频数据来构建每日semi-beta,这种方法允许研究者在一天内捕捉更多的市场信息。具体来说,每日semi-beta的计算公式如下:
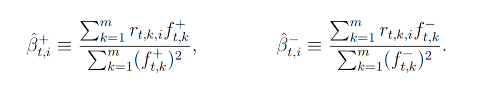
其中,rt,k,i 表示在时间 t 和间隔 k 的资产 i 的回报率,ft,k 表示同期的市场回报率,m 表示一天内的观测次数,而 rt,k,i+ 和 rt,k,i− 分别表示资产回报的正和负部分,ft,k+ 和 ft,k− 同理。
作者使用S&P 500指数成分股的高频数据进行实证分析,覆盖了1993年至2019年的时间跨度。通过这种分析,作者发现每日semi-beta与未来回报之间的关系比基于日回报的月度semi-beta更强。这表明,使用高频数据的semi-beta能够提供关于资产定价更有力的预测。具体结果见下图。
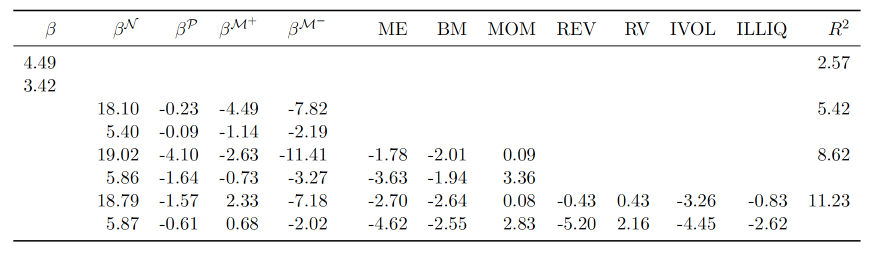
• β (传统市场Beta):年化风险溢价为4.49%
• βN, βP, βM+, βM- (semi-beta):与月频数据相似,βN和βM-的风险溢价显著,分别为18.10%和-7.82%,而βP和βM+的风险溢价不显著。包括semi-beta的模型R²为5.42%,高于仅使用传统市场Beta的2.57%
• 使用高频数据的每日semi-beta在预测未来收益方面显示出更强的能力,这可能是因为高频数据能够更好地捕捉市场的瞬时动态。
对比日频数据的semi-beta可以看到,高频数据能够揭示更为细致的非正态依赖性,这是因为随着采样频率的提高,能够更好地捕捉市场和个别资产之间的瞬时动态关系。
同时高频数据在计算方式上保持不变,但采样的频率提高到了每15分钟一次,从而在每天的交易时间内获得更多的数据点。这符合实现semi-beta理论中的“填充渐近理论”,即随着采样频率的增加,实现semi-beta会更为精确地估计真实的潜在协方差组件。作者同样统计了自相关性,高频数据的semi-beta显示出更强的自相关性,并且与未来收益的关系更为显著。
第五部分将深入探讨基于semi-beta的投资策略,分析如何利用这些新的度量工具来构建投资组合并实现超额回报。
下表展示了基于semi-beta的投资策略的表现,包括“bet on βN”(看好βN)、“bet against βM−”(看空βM−)以及一个组合这两种策略的“Semi-β”策略。这些策略都是基于每日实现的semi-beta构建的,并使用标准普尔500指数成分股进行回测。
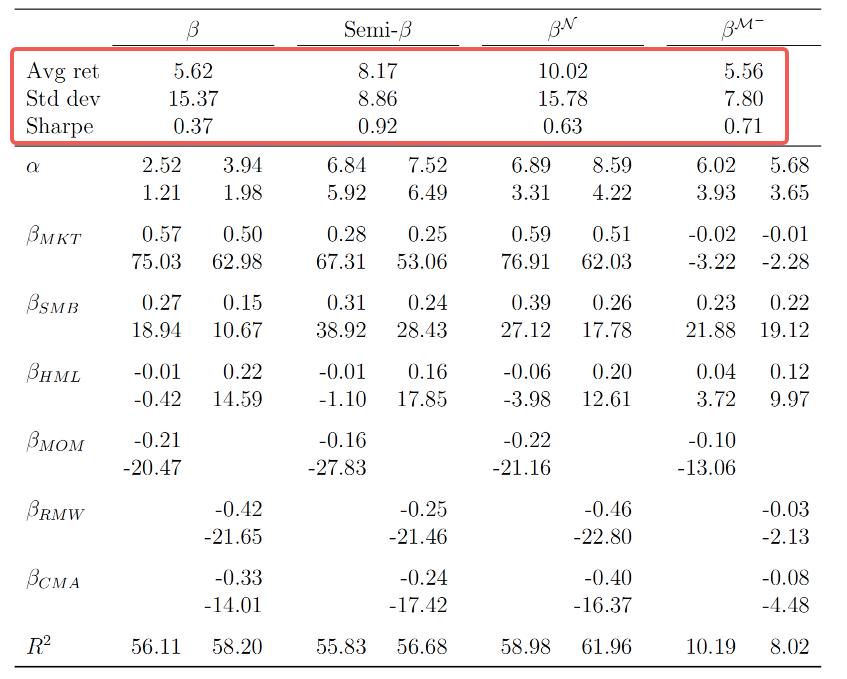
首先从收益上看β策略年化收益为5.62%,Semi-β策略结合了βN和βM−策略,平均年化收益为8.17%,高于单纯的β策略。单独基于βN的策略平均年化收益为10.02%,表明投资者愿意为与市场负收益共同变动的资产支付更高的溢价。单独基于βM−的策略平均年化收益为5.56%,相对较低,但波动性也较小。
夏普方面,Semi-β策略的夏普比率最高,为0.92,远高于β策略的0.37,表明Semi-β策略在风险调整的基础上表现更佳。表格中展示FFC4和FF5模型下的信息比率显示了策略相对于因子模型的超额收益,Semi-β策略的α值显著,表明其在风险调整的基础上能够提供显著的超额收益。
基于semi-beta的投资策略不仅在统计上显著,而且在经济意义上也具有重要价值。特别是Semi-β策略,通过结合βN和βM−,提供了更高的风险调整后收益,这支持了作者关于市场对不同semi-beta定价不同的理论。后文中作者还统计了周频、月频调仓的结果,感兴趣的同学也可以翻阅原文。
这一小节讨论了交易成本对投资策略表现的影响,并提出了一种减少交易成本影响的方法——部分调整策略。
文中假设交易成本与投资组合的换手率成正比,以0.5%的双边交易成本为例进行分析。为了减少交易成本,作者提出了部分调整策略,即每个时期只对投资组合进行部分调整,而不是完全调整到最优权重。
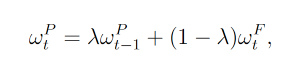
• Pt表示了投资者在时间t持有的投资组合的权重。
• Pt−1表示在时间t−1的部分调整后的权重向量,这个向量表示了投资者在上一期结束时持有的投资组合的权重
• λ为调整速度参数,是一个标量值,范围在0到1之间(0<λ<1)。如果λ接近1,表示权重调整得较慢,投资组合的变化较小;如果λ接近0,表示权重调整得较快,投资组合的变化较大。
• Ft表示在时间t的完全调整后的权重向量,这个向量表示了如果投资者在时间t完全根据新的市场信息调整其投资组合,将会得到的权重。
公式的核心思想是,投资者不会在每个时期完全根据新的市场信息调整其投资组合,而是在保持一部分原有投资权重的同时,只对剩余的部分进行调整。这种方法可以减少频繁交易带来的成本,同时也可以避免因市场短期波动而做出过于剧烈的调整。
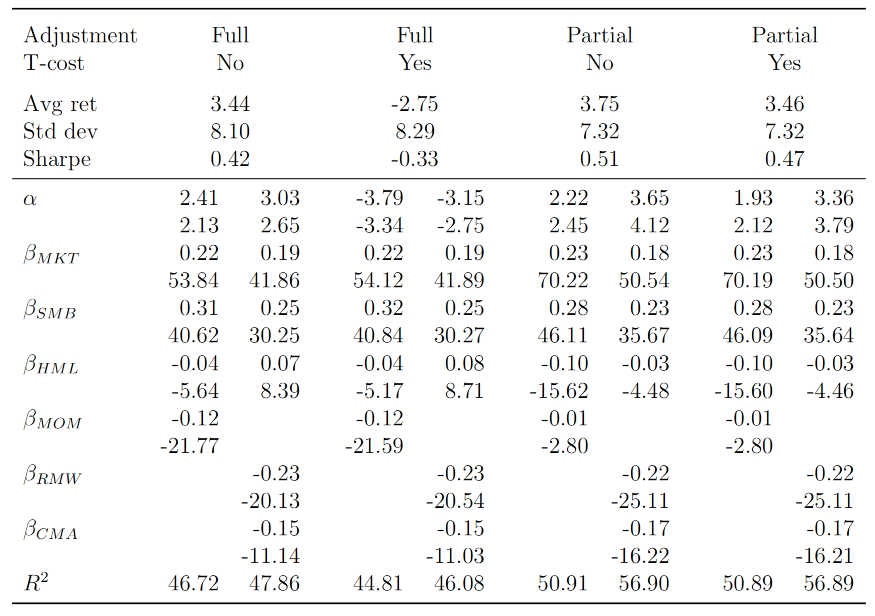
上图展示了在考虑交易成本的情况下,基于semi-beta的投资策略的表现。这些策略包括完全调整(Full)和部分调整(Partial)的Semi-β投资组合,并且考虑了有无交易成本(T-cost)的情况。
• 完全调整且无交易成本的Semi-β策略平均年化收益为3.44%。
• 当引入0.5%的交易成本时,完全调整的Semi-β策略平均年化收益降低至-2.75%,表明交易成本对策略表现有显著影响。
• 部分调整的Semi-β策略在无交易成本时平均年化收益为3.75%,比完全调整的策略表现更好。
• 完全调整的Semi-β策略在无交易成本时夏普比率为0.42,考虑交易成本后降至-0.33,说明交易成本显著降低了风险调整后的收益。
• 部分调整的策略即使在考虑交易成本后,夏普比率仍为正(0.47),表明部分调整策略在控制交易成本方面更为有效。
• 表格展示了投资组合相对于Fama-French四因子和Carhart五因子模型的因子载荷。部分调整策略在控制交易成本的同时,仍保持了与市场和其他因子的相关性。
• 表格中的数据表明,交易成本对投资策略的表现有显著影响,尤其是在完全调整的策略中。
• 部分调整策略通过减少交易频率,降低了交易成本对策略表现的负面影响。此外,部分调整策略还可能减少了semi-beta估计中的“噪声”,从而增强了信号。
• semi-beta的新框架:作者提出了一种新的市场beta分解方法,将传统的市场beta分解为四个semi-beta,这些semi-beta基于市场和个别资产回报之间的有符号协方差。
• 风险溢价的非对称性:文献发现,只有与市场负回报变化相关的两个semi-beta(βN和βM-)具有显著的风险溢价,而与市场正回报变化相关的semi-beta(βP和βM+)则没有显著的风险溢价。
• 市场摩擦和套利风险:作者指出,βN和βM-的风险溢价不同可能是由于市场摩擦和套利风险造成的,这些因素在长和短头寸的风险补偿之间产生了差异。
• 实证分析的一致性:通过不同采样频率、预测期限和多种控制变量的实证分析,作者发现βN的风险溢价大约是βM-的两倍,并且接近传统市场beta风险溢价的三倍。
• 投资策略的有效性:文献展示了基于semi-beta的投资策略,特别是“bet on βN”和“bet against βM-”策略,能够产生显著的超额收益和高夏普比率。
• 交易成本的考虑:即使在考虑交易成本的情况下,基于semi-beta的投资策略仍然能够产生经济上显著和统计上稳健的正alpha。
• 对传统CAPM的扩展:本文的研究结果为传统的资本资产定价模型(CAPM)提供了新的视角,表明市场可能更关注于下行风险,而不是总体方差。
下面是一份简单的semi-beta计算函数,文中给出的semi-beta除了能用来丰富因子库,更为重要的是可以用于组合优化控制风格暴露,已有业界机构在上半年从beta因子这个角度发力,业绩曲线做的很不错,规模也实现逆势增长。
## 以下为4个beta的简单计算## 仅展示计算公式的逻辑,底层数据需自备
def semibeta_pos(dates, index, bar1): bench = '000905.XSHG' index_adj = index.applymap(lambda x: x if x >0 else 0) fac = pd.DataFrame(np.sum(bar1.applymap(lambda x: x if x >0 else 0).values * index_adj.values, axis = 0) / np.sum(index.values ** 2), index = bar1.columns).reset_index() fac.insert(0, 'date', dates) fac.columns = ['date','code','paper_semibeta_pos_min'] filters = bar1.sum() fac.loc[fac[fac['code'].isin(filters[filters == 0.].index)].index, 'paper_semibeta_pos_min'] = np.nan
def semibeta_neg(dates, index, bar1): bench = '000905.XSHG' index_adj = index.applymap(lambda x: x if x < 0 else 0) fac = pd.DataFrame(np.sum(bar1.applymap(lambda x: x if x < 0 else 0).values * index_adj.values, axis = 0) / np.sum(index.values ** 2), index = bar1.columns).reset_index() fac.insert(0, 'date', dates) fac.columns = ['date','code','paper_semibeta_neg_min'] filters = bar1.sum() fac.loc[fac[fac['code'].isin(filters[filters == 0.].index)].index, 'paper_semibeta_neg_min'] = np.nan
def semibeta_market_pos(dates, index, bar1): bench = '000905.XSHG' index_adj = index.applymap(lambda x: x if x > 0 else 0) fac = pd.DataFrame(-1 * np.sum(bar1.applymap(lambda x: x if x < 0 else 0).values * index_adj.values, axis = 0) / np.sum(index.values ** 2), index = bar1.columns).reset_index() fac.insert(0, 'date', dates) fac.columns = ['date','code','paper_semibeta_mpos_min'] filters = bar1.sum() fac.loc[fac[fac['code'].isin(filters[filters == 0.].index)].index, 'paper_semibeta_mpos_min'] = np.nan
def semibeta_market_neg(dates, index, bar1): bench = '000905.XSHG' index_adj = index.applymap(lambda x: x if x < 0 else 0) fac = pd.DataFrame(-1 * np.sum(bar1.applymap(lambda x: x if x > 0 else 0).values * index_adj.values, axis = 0) / np.sum(index.values ** 2), index = bar1.columns).reset_index() fac.insert(0, 'date', dates) fac.columns = ['date','code','paper_semibeta_mneg_min'] filters = bar1.sum() fac.loc[fac[fac['code'].isin(filters[filters == 0.].index)].index, 'paper_semibeta_mneg_min'] = np.nan
发布者:股市刺客,转载请注明出处:https://www.95sca.cn/archives/133973
站内所有文章皆来自网络转载或读者投稿,请勿用于商业用途。如有侵权、不妥之处,请联系站长并出示版权证明以便删除。敬请谅解!

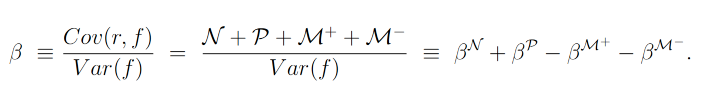
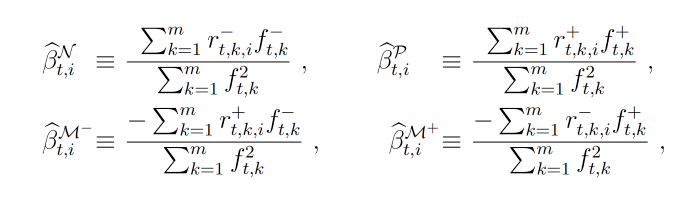

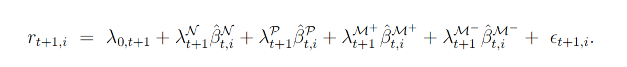

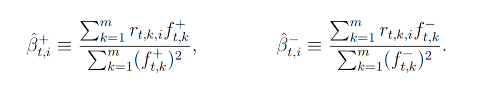


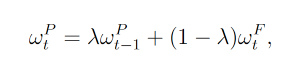



![[通达信指标]BS操盘线趋势线公式](https://95sca.cn/2024/08/07/vo8mzxsZWaVjKnA1722997608.906477.jpg?imageMogr2/thumbnail/!480x300r|imageMogr2/gravity/center/crop/480x300)

![[通达信指标]拉升MACD附图公式](https://95sca.cn/2024/08/07/0KpJQiaicRRXlKQ1722995452.838568.jpg?imageMogr2/thumbnail/!480x300r|imageMogr2/gravity/center/crop/480x300)

