|
《From Factor Models to Deep Learning: Machine Learning in Reshaping Empirical》
https://arxiv.org/pdf/2403.06779v1
前言:本文为框架概念类文章,适合入市未深需要搭建框架类同学
|
| 本文全面回顾了机器学习和人工智能在资产定价领域的应用,探讨了其如何克服传统模型的局限性并提高预测精度。首先总结了传统因子模型及其局限性,然后介绍了各种机器学习模型在资产定价中的应用;接着,探讨了机器学习在投资组合优化中的应用,包括监督学习和强化学习方法。此外,文章还分析了机器学习在资产定价技术中的创新,如降维、缺失数据填充、替代数据整合、降噪和非 IID 适应等。最后讨论了机器学习在资产定价中的挑战,例如数据可用性、市场动态、模型复杂性、监管合规性和模型可解释性等。 |
• 涵盖了从传统因子模型到机器学习模型的演变,并详细介绍了各种机器学习模型在资产定价中的应用。
• 探讨了机器学习在投资组合优化中的应用,包括监督学习和强化学习方法。
• 分析了机器学习在资产定价技术中的创新,如降维、缺失数据填充、替代数据整合、降噪和非 IID 适应等。
• 讨论了机器学习在资产定价中的挑战,如数据可用性、市场动态、模型复杂性、监管合规性和模型可解释性等。
• 提出了未来研究方向,例如在线学习、元学习和集成学习,以提高模型的泛化能力。
• 金融市场受到多种因素的影响,包括宏观经济指标、市场情绪、政策变化等,这些因素相互作用,形成的高度复杂和动态的系统要求更先进的模型来预测资产价格和风险。
• 传统的资产定价模型,如CAPM,假设市场是有效的,并且资产收益与系统性风险(市场风险)线性相关。Fama-French模型虽然扩展了CAPM,增加了规模、价值、盈利能力和投资风格等因素,但仍然存在预测准确性不足、变量选择困难和函数形式不够灵活的问题。
• 机器学习模型(包括监督学习、无监督学习、半监督学习)和强化学习,能够整合异构数据源,如文本、图像和音频数据,这些数据源为金融分析提供了新的视角和信息。
传统因子模型回顾
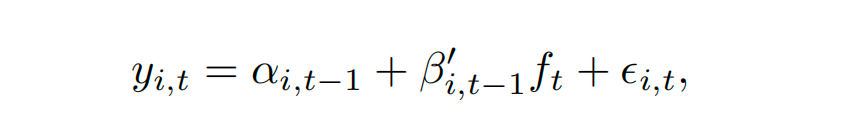
以上公式为因子模型的基本结构。其中,yi,t 是资产i在时间t超过无风险利率的超额回报,αi,t−1 是资产特定风险的补偿,βi,t−1′ 是资产i对因子的敞口,ft 是风险因子,ϵi,t 是误差项。
• 因子模型是资产定价中的核心,它们基于一个基本理念:可以通过少量因子来解释资产收益率的横截面差异。
• 这些因子代表了资产对某些共同风险因素的敞口,而资产特定的风险可以通过alpha系数表示。
• 传统因子模型通常依赖于线性关系,并且需要事先对影响回报的因素有深入的了解。
机器学习模型在资产定价中的应用
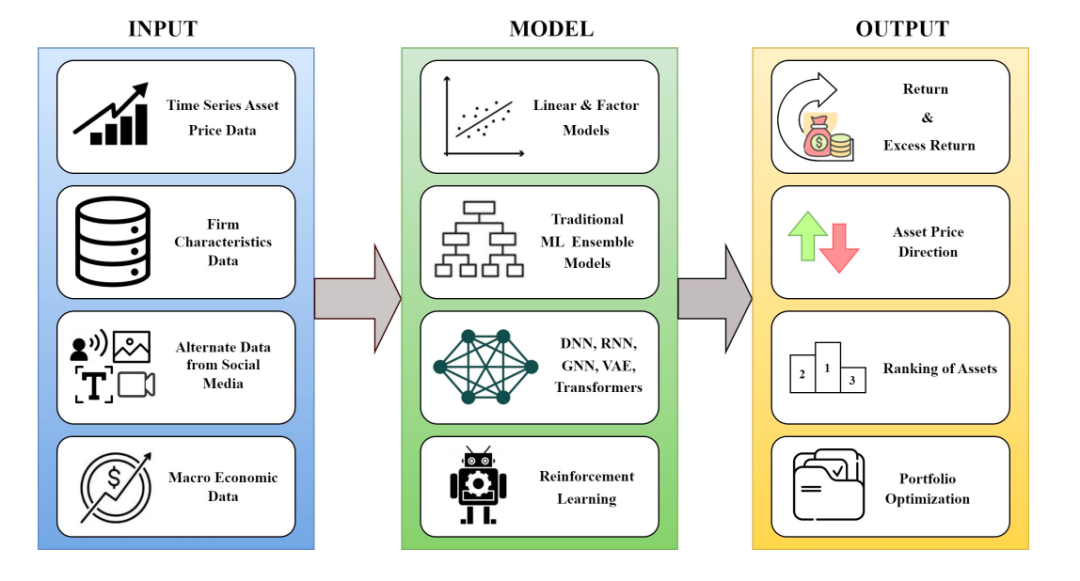
• 风险溢价是预期回报与无风险回报之间的差额,是投资者为承担额外风险而要求的补偿。在资产定价中,准确估计风险溢价对于投资决策至关重要。
• 机器学习模型提供了一种更为灵活的方法来捕捉资产定价中的非线性关系和复杂动态。
• 机器学习模型通过从历史数据中学习,尝试预测未来的超额回报。这些模型包括:
|
线性回归模型:基础方法,假设资产回报与因子之间存在线性关系。
决策树和随机森林:通过构建决策规则从数据特征中学习,能够捕捉非线性关系。
梯度提升回归树:通过迭代地添加弱预测模型来最小化损失函数,提高预测精度。
|
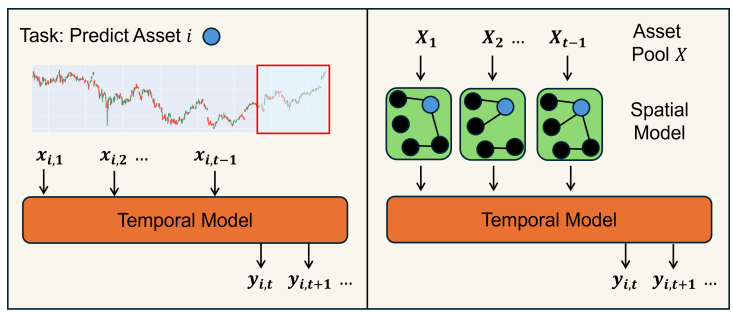
机器学习模型中一个重要的分支为时间序列模型,时间序列模型专注于利用历史价格数据来预测未来的市场趋势,常被用于捕捉时间序列数据中的长期依赖关系,常见模型如ARIMA模型。时序预测公式如下:
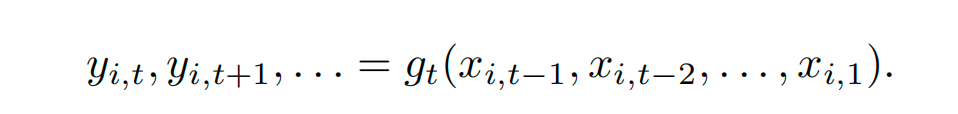
上式中的gt是一个映射函数,它将过去的观察结果xi,t−1,xi,t−2,…,xi,1映射到未来的预测值yi,t,yi,t+1,…。这个函数需要能够捕捉时间序列数据中的动态和依赖性。
此外,本文还介绍了深度学习模型在资产定价中的应用,如长短期记忆网络(LSTM)和Transformer模型。这些模型能够处理高维数据和复杂的非线性关系。
• 处理复杂关系:能够捕捉金融市场的复杂非线性和时间依赖性。
• 处理高维数据:适合处理包含大量特征和观测值的金融数据。
• 自适应特征学习:能够自动提取和选择最重要的特征,提高模型的泛化能力。
投资组合优化是资产定价中的一个关键组成部分。投资者通过构建包含多种资产的投资组合来实现风险和收益的最佳平衡。现代投资组合理论(MPT)提出,投资者可以通过分散投资来降低风险,从而实现更优的风险收益比。本文探讨了机器学习在投资组合优化中的应用,主要包括监督学习和强化学习方法。
监督学习模型可以通过估计资产的预期回报和协方差矩阵来辅助投资组合优化。具体方法包括:
1. 资产选择:利用回归模型预测资产的未来回报,选择预期回报最高的资产进行投资。公式如下:
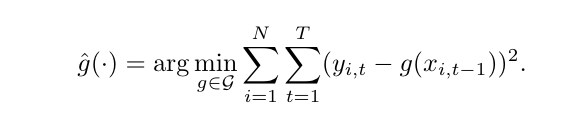
上面公式中的优化问题是一个损失最小化问题,其中g是模型需要学习的函数,G是所有可能的函数集合,N是资产数量,T是时间序列的长度。目标是找到最优的g^,使得所有资产在所有时间点上的预测误差之和最小。
2. 投资组合构建:根据预测结果构建多空组合,即买入预期回报高的资产,卖出预期回报低的资产。投资组合的权重可以通过等权重或基于预测结果的加权方式确定。
强化学习(RL)是一种通过试错学习最优策略的方法,适用于投资组合优化。RL的核心是通过神经网络近似动作策略函数和奖励函数,公式如下:
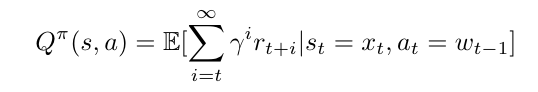
其中,st 是状态,at 是动作(即投资组合权重),rt 是奖励(即对数回报),γ 是折扣因子。
• 状态表示:状态 st 通常表示为历史价格和投资组合权重的组合。
• 动作选择:通过神经网络确定投资组合权重向量 wt。
• 奖励函数:奖励 rt 通常是周期性的对数回报。
在资产定价中,经常面临大量的预测因子,这可能导致模型复杂度增加和过拟合风险。降维技术可以帮助简化模型,提取出最有预测力的因子。
• 主成分分析(PCA):通过正交变换将原始数据投影到新的坐标系,使得数据的最大方差由第一个坐标(主成分)表示。PCA可以有效减少数据的维度,避免过拟合,同时保留最重要的信息。
• 自编码器:通过神经网络训练,将输入数据压缩到低维隐空间,然后再解码回原始空间。自编码器能够学习数据的潜在表示,适用于处理高维和非线性数据。
• 变分自编码器(VAE):结合概率模型和深度学习的优点,通过变分推断进行特征提取和数据生成。VAE能够处理低信噪比的金融数据,提供更有意义的潜在因子。
金融数据常常包含缺失值,这可能影响模型的性能。缺失数据填充技术可以提高数据质量,使模型能够更好地学习。
• 矩阵分解:通过分解用户-项目评分矩阵来预测缺失评分。矩阵分解方法能够有效利用用户和项目之间的潜在关联,恢复丢失的评分信息。
• 基于变换器的模型:利用Transformer架构处理缺失数据,通过自注意力机制捕捉数据中的依赖关系。基于变换器的模型能够处理复杂的非线性关系,提供高精度的缺失数据填充。
另类数据整合是指将非传统的金融数据(如文本、图像、语音等)与传统财务信息相结合,以提高资产定价模型的准确性和复杂性。
文本数据包括公司描述、社交媒体内容等,这些数据在投资推荐和市场分析中具有重要作用。例如,时间感知图关系注意力网络(TRAN)将文本内容与财务数据集结合,用于增强股票分析和推荐系统。预测-解释网络(PEN)强调了社交媒体输入、股票间关系动态和传统财务指标的协同作用,特别是情感分析在提高股票运动预测准确性方面的重要性。
图像分析在金融数据处理中也显示出显著的优势。例如,Cohen et al. [2020] 将时间序列分析重新定义为图像分类任务,使用卷积神经网络(CNN)进行市场动态分析。Zeng et al. [2021] 将多个资产的价格数据转换为二维图像,并利用视频预测算法进行市场动态分析。
语音数据在资产定价中的应用也取得了显著进展。例如,VolTAGE 模型[Sawhney et al., 2020] 将公司高管收益电话中的语音线索与传统财务数据结合,在图卷积网络(GCN)中进行分析。该模型使用多模态、多话语注意力机制,展示了数据综合的全面方法。
金融数据是众所周知的信噪比极低,而降噪就是在金融数据预测中去除噪声,以提高模型的预测精度。非 IID 适应是指处理金融数据中不符合独立同分布(IID)假设的情况。
对比学习最初在计算机视觉任务中取得成功,现已被应用于金融领域以提高模型的预测能力。例如,基于Copula的对比预测编码(Co-CPC)[Wang et al., 2021a] 通过对比连续时间点的数据来过滤噪声并增强股票表示。对比多粒度学习框架(CMLF)[Hou et al., 2021] 使用双重对比方法处理数据粒度和时间关系的复杂性,从而提高预测准确性。
专家混合模型(MoE)是一种在大规模语言模型(LLMs)中领先的技术,通过一组专门的子模型或“专家”来解释特定的数据模式或市场条件,克服了传统的一刀切方法。例如,时间路由适配器(TRA)[Lin et al., 2021] 优化了数据到预测器的分配,促进了时间模式的准确识别,而模式自适应专家网络(PASN)[Huang et al., 2022] 通过模式自适应训练促进了对新市场动态的自主适应。
数据可用性和质量
• 金融数据的专有性和获取成本较高,导致研究者往往只能访问有限的数据集,这限制了模型的测试和验证。
• 现有研究多集中在历史数据上,对债券和衍生品等其他市场的关注不足。
• 建立一个全面的数据集或合成数据集,反映金融市场的复杂性,对于健壮和公平的模型评估至关重要。
|
市场动态和结构变化
• 金融市场受到经济不确定性、地缘政治事件和投资者行为假设的影响,呈现出时间变化的动态和结构性变化。
• 无套利理论指出,任何能够识别错误定价的模型都会迅速使这种错误定价消失。
• 在线学习和元学习可以作为模拟不断演变的金融景观的一步,用于建模结构变化。可以看我的这篇文章
|
模型复杂性和过拟合风险
|
• 深度学习模型在训练数据上表现良好,但在未见过的数据上可能表现不佳,这表明存在过拟合的风险。
• 研究使用元学习、一次性学习和集成学习算法,结合早停和dropout技术,开发更泛化的资产定价模型。
|
监管合规性
|
• 金融行业受到严格的监管要求,包括透明度、问责制和遵守既定准则。
• AI算法需要符合GDPR、MiFID II和Basel III等法规,这需要文档化、鲁棒性高的验证和持续监控。
• 金融、AI开发和监管机构之间的合作可以促进道德AI原则的实施,并在AI驱动的金融领域促进透明度。
|
模型可解释性和公平性
|
• 深度学习模型因其“黑箱”特性和算法偏见而受到批评。
• 监管机构和投资者越来越关注模型的可解释性和公平性,而不仅仅是预测准确性。
• 可解释人工智能的兴起代表了这一方向的重要进步。未来的研究可以探索可解释性和性能之间的平衡,为金融模型提供更大的透明度。
|
发布者:股市刺客,转载请注明出处:https://www.95sca.cn/archives/133972
站内所有文章皆来自网络转载或读者投稿,请勿用于商业用途。如有侵权、不妥之处,请联系站长并出示版权证明以便删除。敬请谅解!
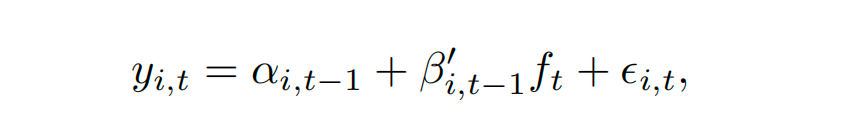

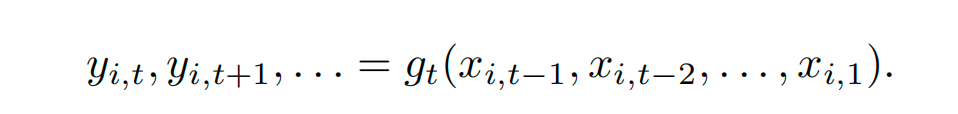
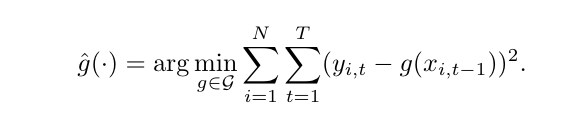
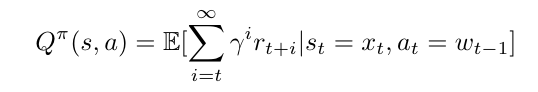


![[通达信指标]大主力驱动主图公式](https://95sca.cn/2024/08/07/WJr25EGLPsY16NQ1722996201.8561285.jpg?imageMogr2/thumbnail/!480x300r|imageMogr2/gravity/center/crop/480x300)
![[通达信APP指标]红蓝波段顶底附图公式 手机可用](https://95sca.cn/2024/08/07/heL6f6y0ZWXicCw1722996551.8014665.jpg?imageMogr2/thumbnail/!480x300r|imageMogr2/gravity/center/crop/480x300)


