AFS-BM：一种自适应数据变化的二进制掩码特征选择[附开源代码]

一 本文简介

随着数字时代的到来，我们面临着大量的高维数据，其中包括基因组学和金融领域的数据。这些数据集对于机器学习和模型开发非常有价值，但也带来了一些挑战。高维数据意味着特征的数量很多，这可能导致模型过于复杂、计算资源消耗大，且难以解释模型的结果。因此，特征选择变得非常重要，它可以帮助我们识别出对于我们任务最重要的特征，去除不必要的特征，提高模型的效率和准确性。特别是在数据有限的情况下，特征选择可以起到关键的作用。然而，特征选择也是一个挑战，尤其是在高维和非平稳的环境下。在这种情况下，我们需要找到一种方法来自动地选择相关的特征，并且能够适应数据的变化。

本文提出了一种新的特征选择方法：自适应二进制掩码特征选择（AFS-BM）。这种方法结合了特征选择和模型训练，通过调整二进制掩码和模型参数来实现。AFS-BM的优势在于它能够动态地选择特征，并且可以处理数据不足的情况。通过集成二进制掩码，我们可以同时微调特征集并增强模型训练，从而更敏捷高效地识别相关特征。这种方法在实验中表现出稳健和有效的特点，并且相比传统的特征选择技术，能够带来显著的性能改进。

二 背景知识

特征选择在机器学习中扮演着关键的角色。它帮助我们从原始数据中选择最相关的特征，以提高模型的性能和可解释性。正确选择特征可以减少模型的复杂性、降低过拟合的风险，并提高模型对真正相关数据的关注度。

2.1 特征选择问题定义

特征选择是在给定一个特征集合的情况下，通过评估和排除不相关或冗余特征，选择出最具预测能力的特征子集的过程。

问题定义如下：

给定一个包含N个样本的数据集，每个样本包含M个特征。我们的目标是从这M个特征中选择出一个最佳的特征子集，使得这个子集中的特征能够最好地解释或预测目标变量。

特征选择的问题可以分为三个主要方面：

1. 目标变量：我们需要明确选择特征的目标是什么。是为了解释目标变量的变化，还是为了预测目标变量的值。
2. 特征评估：我们需要确定如何评估每个特征与目标变量之间的关联程度。常用的评估方法包括统计检验、相关系数、信息增益等。
3. 特征子集搜索：特征选择的最终目标是找到一个最佳的特征子集，其中包含与目标变量强相关的特征，并且特征之间尽可能不相关或冗余。搜索特征子集的方法可以是贪婪搜索、遗传算法、回溯法等。

特征选择的目的是减少特征空间的维度，提高模型的性能、降低过拟合风险，同时也可以提高模型的解释性和可解释性。通过选择最相关的特征子集，我们可以获得更简洁、更有效的模型，并且更好地理解数据中的关键因素。

2.2 常见的特征选择方法

• 使用GBMs进行特征选择：当使用GBMs进行特征选择时，可以通过计算特征的SHAP值来衡量其在模型中的重要性。SHAP值是通过对比不同特征子集的预测结果，计算特征对预测结果的边际贡献。通过这种方式，我们可以识别并舍弃那些对预测结果贡献较小的特征。
• 递归特征消除 (RFE)：递归特征消除是一种特征选择的方法，通过逐步地剪枝较不重要的特征来优化机器学习模型。它的核心思想是从最初的特征集合开始，通过训练模型并评估特征的重要性，逐步移除对模型贡献较小的特征。这样可以使模型更加专注于最相关的特征，提高模型的性能和泛化能力。
• 使用贪婪方法进行特征选择：贪婪方法是一种特征选择的方法，它根据特征之间的相关性和信息量来选择特征。其中，互相关和互信息是两种常用的度量方法。互相关是一种度量两个特征之间线性关系强弱的方法。通过计算两个特征之间的协方差和标准差，可以得到它们的互相关系数。较高的互相关系数表示两个特征之间存在较强的线性关系，较低的互相关系数表示它们之间关系较弱或无关。互信息是一种度量两个随机变量之间相关性的方法。它衡量了一个变量中的信息对另一个变量的预测能力。较高的互信息表示两个变量之间有较强的相关性，较低的互信息表示它们之间关系较弱或无关。通过使用贪婪方法中的互相关和互信息度量，我们可以评估特征之间的相关性，并选择那些与目标变量相关性较高的特征进行建模和预测。这有助于减少特征空间的维度，提高模型的效果和解释能力。

2.3 当前方法存在的问题

当前特征选择方法的问题在于它们通常是静态的，无法适应数据的变化和复杂模型的需求。首先，过滤方法虽然简单，但它们忽略了特征之间的相互关系，可能会选择出具有高度相关性的特征，导致冗余信息。其次，包装方法需要在每个特征子集上运行机器学习算法，计算成本高昂，不适用于大规模数据集。此外，嵌入方法将特征选择整合到模型训练中，但它们可能受限于所选择的模型类型，不适用于所有机器学习算法。

另一个问题是在处理高维和非平稳数据时，现有方法的效果有限。在高维数据集中，特征数量庞大，可能存在大量无用的特征，这会导致过拟合和模型性能下降。而传统的特征选择方法往往无法处理这种情况，难以准确地选择出对模型有益的特征。此外，非平稳数据指的是数据分布或特征之间的关系可能随时间变化，这就要求特征选择方法能够适应数据模式和关系的变化，以保持模型的稳健性和相关性。

三 本文贡献

本文提出的AFS-BM是一种新的特征选择方法，具有以下优势：

• 动态适应性：AFS-BM使用二进制掩码和迭代优化技术，能够动态地调整特征的重要性。它可以根据数据的变化灵活地选择特征，使模型保持稳健和相关。
• 高维数据处理：AFS-BM通过迭代优化识别和保留最相关的特征，减少模型的噪声和复杂性。这使得它在处理高维数据集时表现更好，降低过拟合的风险。
• 适应复杂模型：AFS-BM能够适应复杂模型（如GBM和神经网络）的需求，提高这些模型的性能和可解释性。它不断评估和调整特征的重要性，使模型更关注真正具有预测性的特征。
• 提高模型性能和可解释性：由于AFS-BM精确选择特征，减少噪声和复杂性，它能够提高模型的性能和可解释性，使结果更准确且更容易理解。

四 本文方法

自适应二进制掩码特征选择方法（AFS-BM）是一种通过优化二进制掩码来改进特征选择的方法。它的原理如下：

1. 首先准备一个数据集，其中包含许多样本。每个样本都有一组特征和一个目标值。
2. 定义一个二进制掩码，它有与特征数量相同的位数，每个位代表一个特征。通过将特征向量与二进制掩码进行修改，通过特征掩码可以选择特定的特征或舍弃特定的特征。
3. 定义一个目标函数，它由两部分组成。第一部分是模型的损失函数，它衡量模型预测结果与真实目标值之间的差异。第二部分是二进制掩码的L1范数，它衡量所选择的特征的数量。
4. 使用迭代优化算法来不断调整二进制掩码和模型参数，以最小化目标函数。在每次迭代中，我们根据当前的二进制掩码来更新模型参数，并根据模型的性能来调整二进制掩码。
5. 通过不断优化二进制掩码和模型参数，AFS-BM方法可以动态地选择和舍弃特征，从而提高模型的准确性。它能够从大量的特征中提取出最重要的特征，减少了冗余和噪音的影响，提高了模型的性能和可解释性。

模型优化阶段：

模型优化阶段主要是为了微调模型。这个阶段的关键是使用前一次迭代的二进制掩码来确定特征子集，然后创建一个被掩码处理过的数据集。我们的目标是通过减小损失函数来优化模型，在优化后，我们计算测试损失并与基准损失进行比较。

在算法的主循环中，我们使用二进制掩码z(k-1)来确定特征子集，该掩码在上一次迭代中表现最好，即使得模型的损失或错误最小。然后，我们使用该掩码对特征向量进行掩码，并用于模型的训练。训练过程中，我们保持掩码不变，只优化模型的参数。

在优化模型之后，我们使用当前最佳参数来计算测试损失值，并将其作为后续阶段的参考点或阈值。为了计算测试损失，我们使用掩码特征选择数据集作为测试集，并使用最新的最优掩码对特征向量进行掩码。然后，我们计算测试损失值，并将其作为阈值。

通过计算阈值损失，我们进入下一个阶段，即掩码特征选择阶段。在这个阶段，我们将使用阈值损失作为参考，根据特征的重要性选择合适的特征子集，以进一步提高模型的性能和可解释性。

掩码优化和特征选择阶段：

首先是掩码优化阶段。在这个阶段，算法通过迭代地掩码特征并观察对模型损失的影响来区分必要的和冗余的特征。它使用一个临时掩码来评估特征的相关性。通过不断调整临时掩码，直到特征集稳定，算法能够找到在给定数据集上最重要的特征，以实现最小的损失。

接下来是特征选择阶段。在这个阶段，算法使用一个松弛变量来指导优化的持续时间。它从一个初始的临时掩码开始，并根据高斯分布选择唯一的特征索引。所选的特征被从临时掩码中移除，并生成更新的临时特征向量。然后，算法计算新的损失，并判断特征的相关性。只有当损失减少程度小于预定义的阈值时，特征才被认为是相关的。

AFS-BM算法通过掩码优化和特征选择相结合的方式，能够从数据中提取最重要的特征，并减少冗余特征的影响。这样可以提高模型的性能和泛化能力。

AFS-BM算法的伪代码如下：

五 实验总结

5.1 合成数据集实验

为了验证我们的模型在特征选择方面的能力，我们进行了一系列实验。首先，我们使用了一个合成数据集，并使用了AFS-BM算法和其他常见的特征选择方法进行比较。这个合成数据集包含了300个样本和100个特征，其中每个样本只有前10个特征对其有信息贡献。我们通过一个数学公式来生成目标变量向量y，其中包含了特征矩阵X的各种数学运算和高斯噪声。

在实验中，我们将数据集分成了测试集、掩码验证集和模型验证集。为了突出特征选择的重要性，我们没有使用任何特定的特征选择技术，而是使用了LightGBM和XGBoost的默认配置。我们将我们的算法与交叉相关、互信息和RFE等常见的特征选择方法进行了对比。为了得到最佳结果，我们使用验证集对LightGBM、XGBoost和特征选择方法的超参数进行了优化。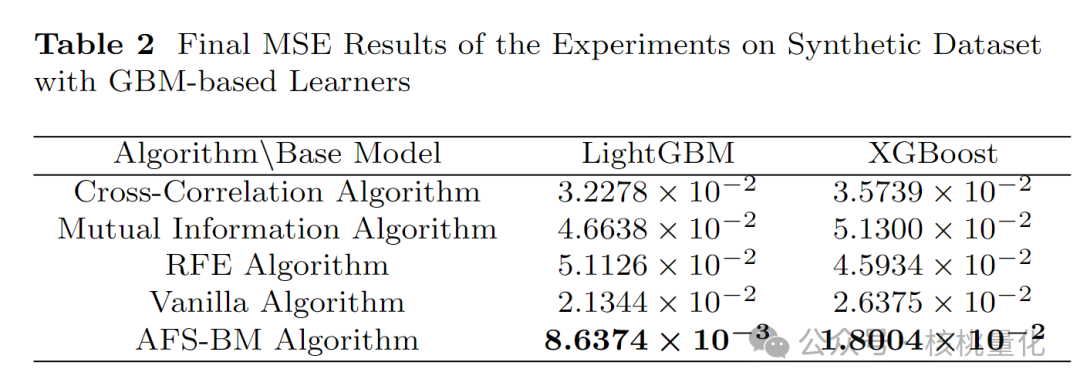


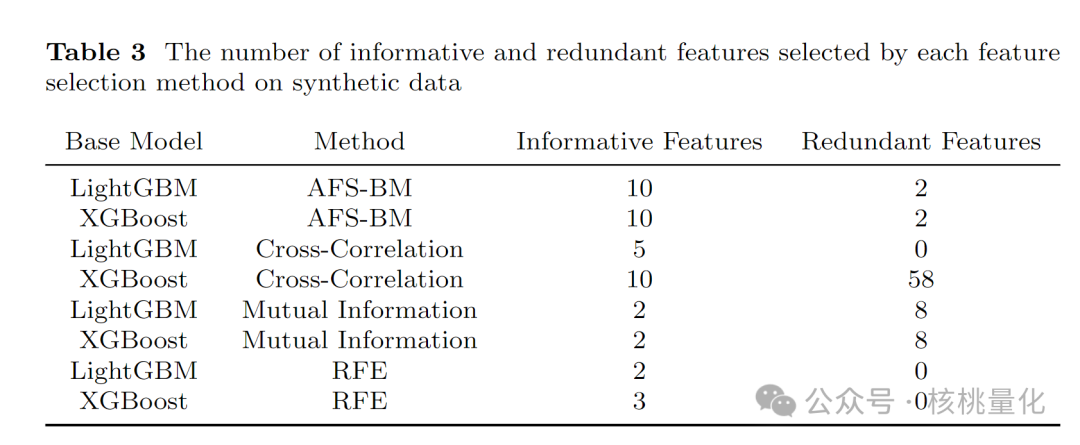
通过表2实验结果，我们发现基于LightGBM和XGBoost的AFS-BM方法能够识别出10个有信息的特征和2个冗余特征。由于高斯噪声的存在，这些冗余特征可能无法被完全消除。需要注意的是，AFS-BM方法收敛到一个包含12个特征的子集，而不需要事先确定选择的特征数量。这意味着它可以在没有关于数据集的先前信息的情况下识别出相关特征。互信息方法能够捕捉非线性关系，但它不利用模型，因此可能与实际情况不匹配。交叉相关方法无法准确表示非线性关系，我们的实验结果也支持这个结论。RFE方法利用模型的特征重要性属性来选择特征，但在准确识别正确特征方面存在一定局限性。

5.2 回归任务实验

我们使用了M4 Forecasting Competition数据集中的日常系列数据来预测目标值yt。为了进行特征工程，我们考虑了yt的前三个滞后值和第7、14和28个滞后值。除了这些基本的滞后特征之外，我们还计算了滚动均值和滚动标准差。为了避免对特定时间序列的偏见，我们选择了100个随机序列，并对它们进行了归一化处理。对于每个随机选择的时间序列，我们应用了所有算法进行特征选择，并计算了测试损失。最终，我们计算了平均平方误差，代表了所有时间序列的预测性能。基于LightGBM的算法的结果显示在图1中，而基于XGBoost的算法的结果显示在图2中。此外，表4提供了我们的算法与标准的LightGBM、XGBoost以及它们与交叉相关、互信息和RFE算法的实现之间的详细比较。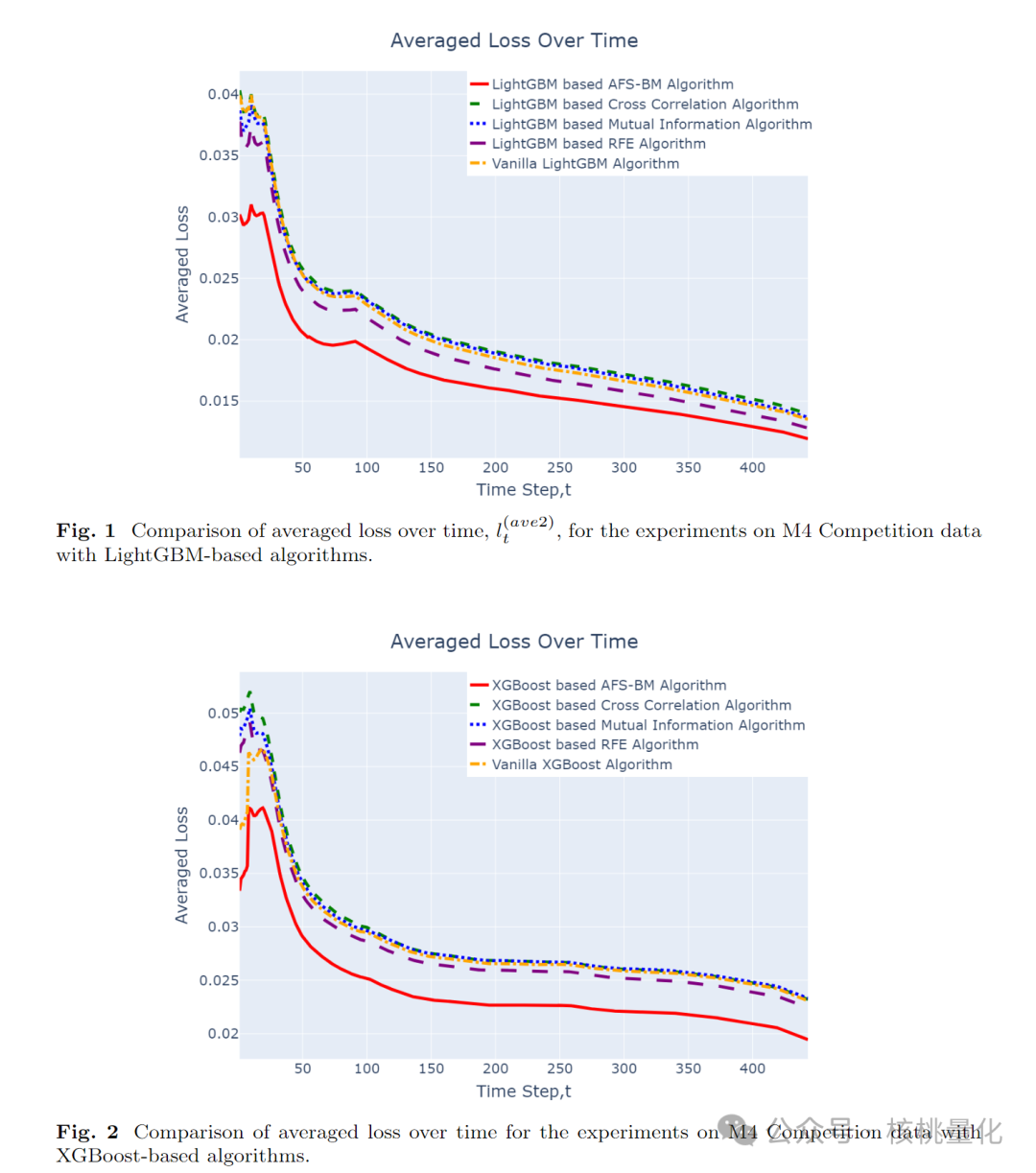

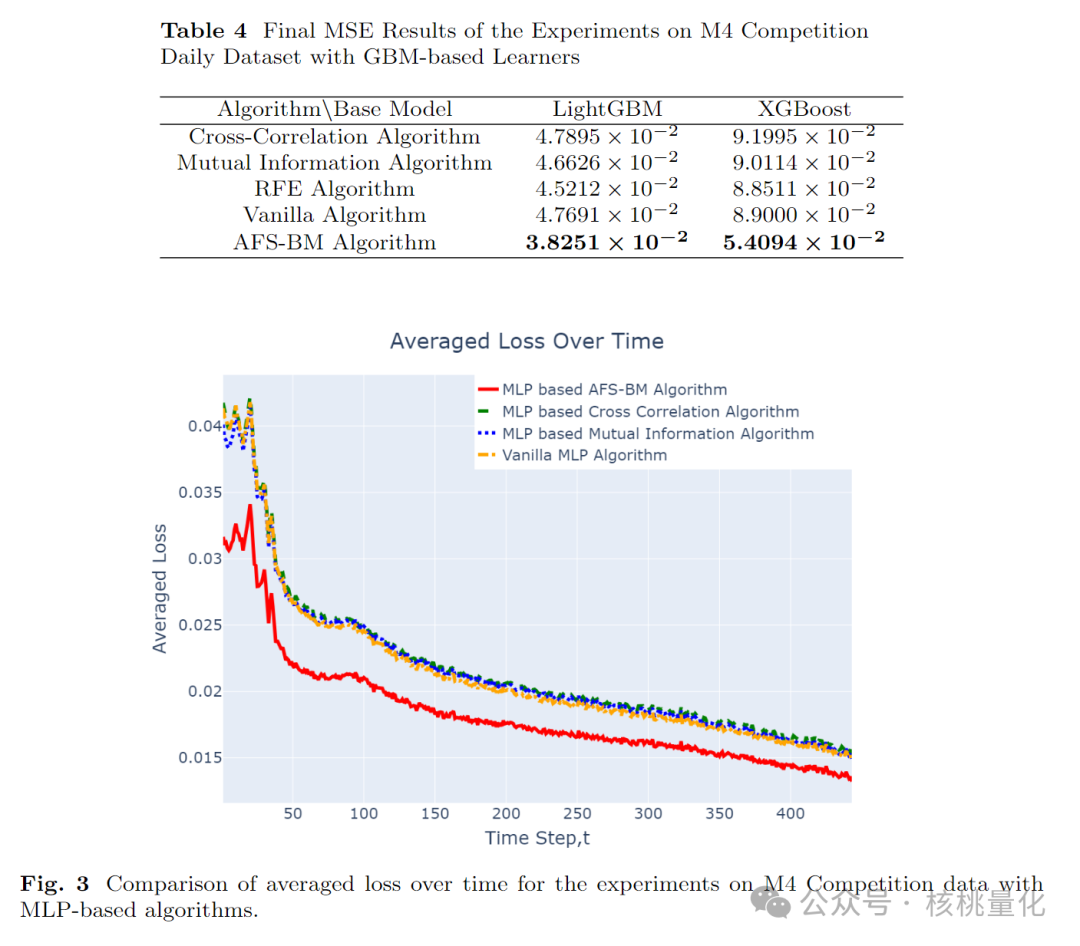
5.3 分类任务实验

我们使用了DARWIN Alzheimer’s病分类数据集来测试我们的AFS-BM算法的性能。我们将我们的算法与使用LightGBM、XGBoost和MLP的其他常见方法进行了比较，并通过调整超参数来获得最佳结果。我们通过表9、10和11展示了结果，表明AFS-BM在分类准确性方面表现出色。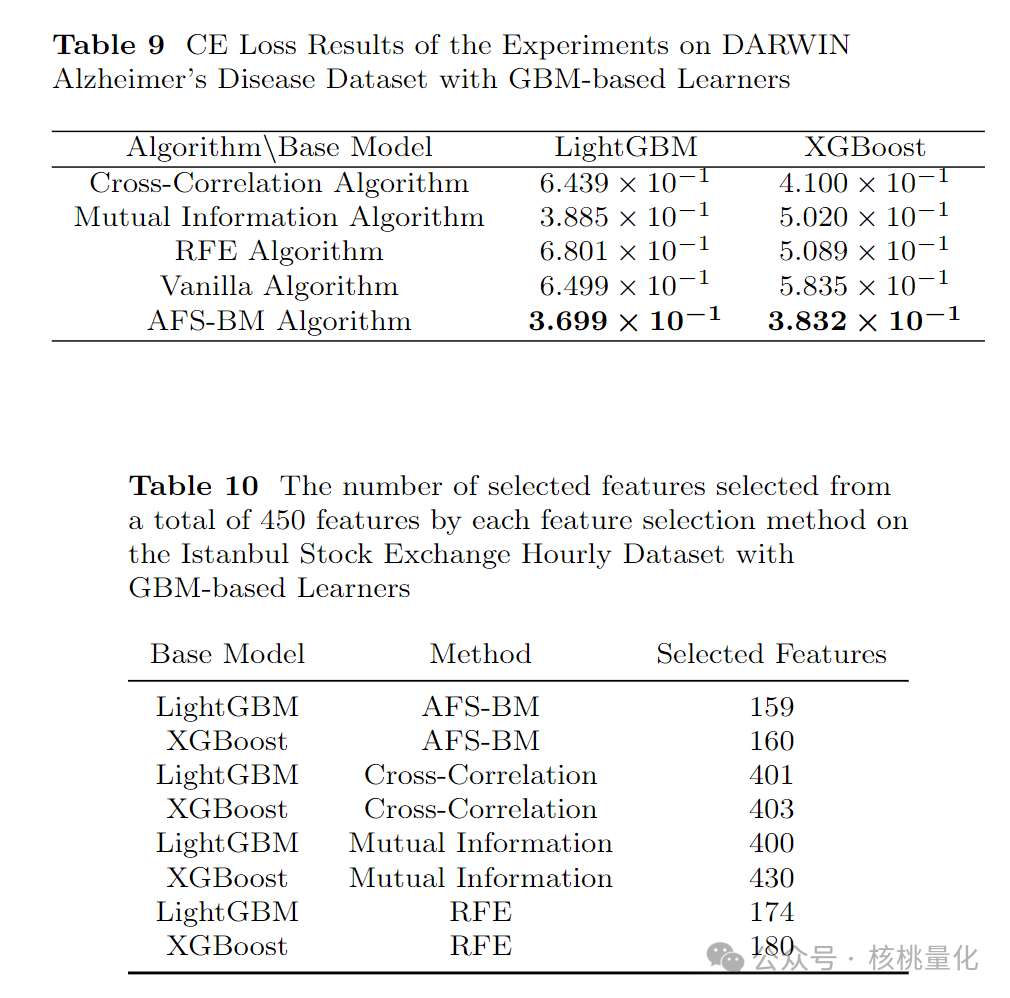

六 总结展望

本文提出了一种新的特征选择方法：自适应二值掩码特征选择（AFS-BM）算法。与传统方法相比，AFS-BM算法通过联合优化动态和随机特征选择以及模型训练，利用二值掩码的方法实现特征的连续调整，以适应特征重要性的变化。与仅仅依靠特征重要性的方法相比，AFS-BM能够更准确地保留关键特征，提高模型的准确性。通过在真实竞赛数据集上的实验证明了AFS-BM算法在特征选择方面的卓越性能。

未来的研究可以进一步探索AFS-BM算法在不同领域和数据集上的适用性，并与其他特征选择方法进行比较。此外，可以考虑将AFS-BM算法与其他机器学习任务结合，如回归、聚类等，以进一步扩展其应用范围。