线段是缠论中非常重要的概念,也是最难的部分,可以说如果把线段学好,那么缠论学习也没太大难度。因此掌握线段的定义和划分原则,非常关键。
一、线段定义
线段至少有三笔,前三笔必须有重叠。
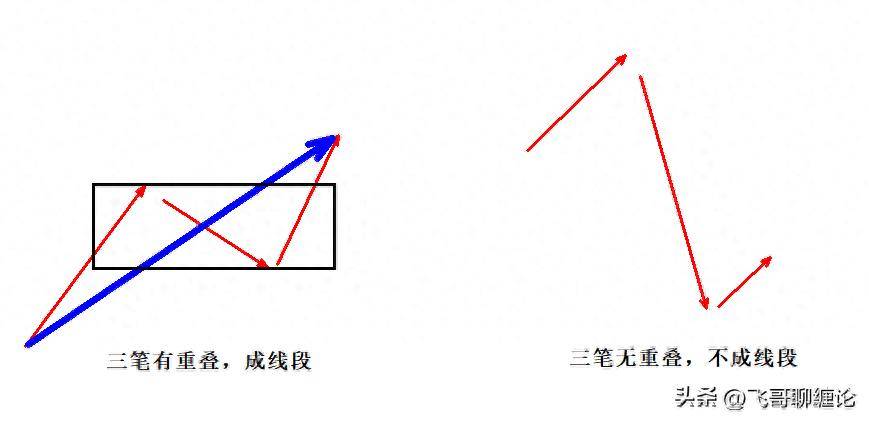
二、线段被笔破坏
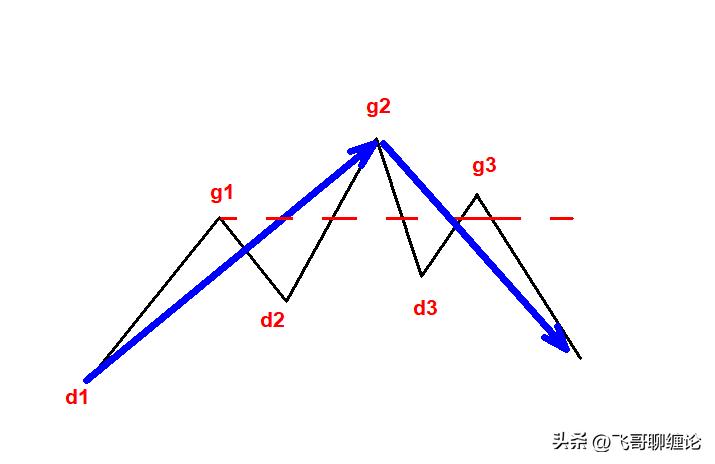
对于从向上一笔开始的,其中的分型构成这样的序列:d1g1d2g2d3g3…dngn(其中 di 代表第 i 个底,gi 代表第 i 个顶)。如果找到 i 和 j,j>=i+2,使得 dj<=gi,那么称向上线段被笔破坏。
如下图所示,d3<g1,那么线段d1g2就被笔g2d3破坏。
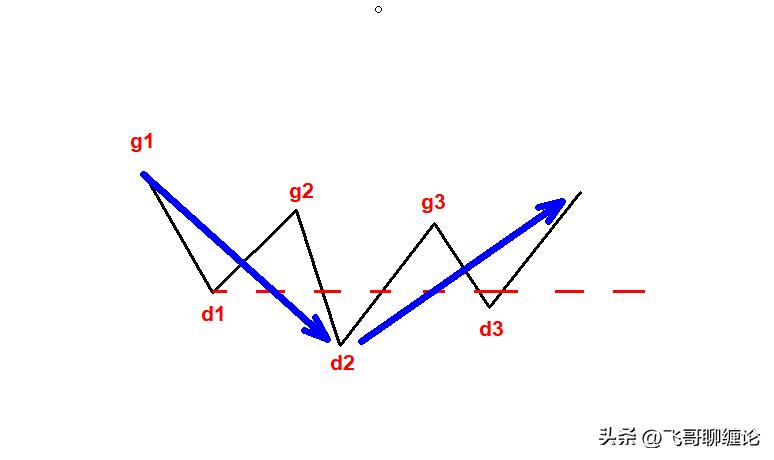
对于从向下一笔开始的,其中的分型构成这样的序列:g1d1g2d2…gndn(其中 di 代表第 i 个底,gi 代表第 i 个顶)。如果找到 i 和 j,j>=i+2,使得 gj>=di,那么称向下线段被笔破坏。
如下图所示,g3>d1,那么线段g1d2就被笔d2g3破坏。
缠中说禅线段分解定理:线段被破坏,当且仅当至少被有重叠部分的连续三笔的其中一笔破坏。而只要构成有重叠部分的前三笔,那么必然会形成一线段,换言之,线段破坏的充要条件,就是被另一个线段破坏。
三、线段划分
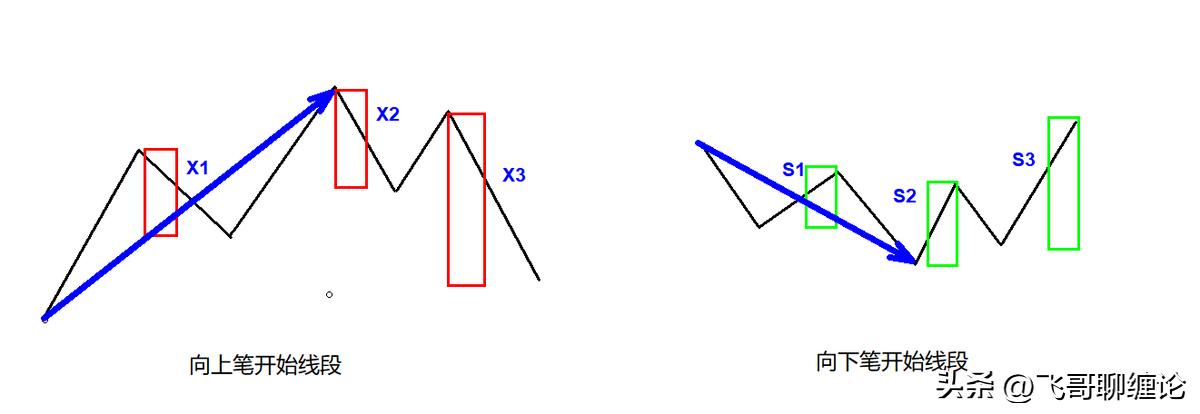
用S 代表向上的笔,X 代表向下的笔。那么所有的线段,无非两种:一、从向上笔开始;二、从向下笔开始。简单起见,以向上笔开始的线段为例子说划分的标准。
以向上笔开始的线段,可以用笔的序列表示:S1X1S2X2S3X3…SnXn。容易证明,任何 Si与Si+1 之间,一定有重合区间。而考察序列 X1X2…Xn,该序列中, Xi 与 Xi+1 之间并不一定有重合区间,因此,这序列更能代表线段的性质。
定义:序列 X1X2…Xn 成为以向上笔开始线段的特征序列;序列 S1S2…Sn 成为以向下笔开始线段的特征序列。特征序列两相邻元素间没有重合区间,称为该序列的一个缺口。
关于特征序列,把每一元素看成是一 K 线,那么,如同一般 K 线图中找分型的方法,也存在所谓的包含关系,也可以对此进行非包含处理。经过非包含处理的特征序列,成为标准特征序列。
参照一般 K 线图关于顶分型与底分型的定义,可以确定特征序列的顶和底。注意,以向上笔开始的线段的特征序列,只考察顶分型;以向下笔开始的线段,只考察底分型。
在标准特征序列里,构成分型的三个相邻元素,只有两种可能:
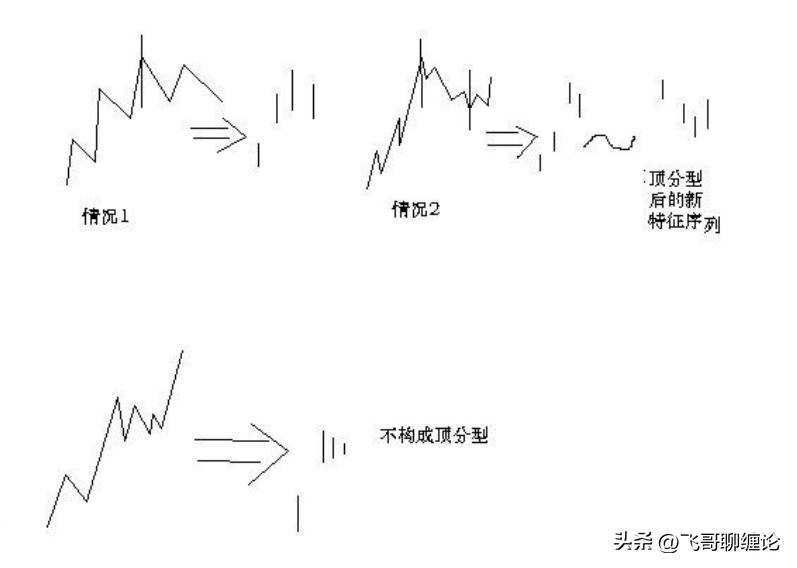
第一种情况:特征序列的顶分型中,第一和第二元素间不存在特征序列的缺口,那么该线段在该顶分型的高点处结束,该高点是该线段的终点;特征序列的底分型中,第一和第二元素间不存在特征序列的缺口,那么该线段在该底分型的低点处结束,该低点是该线段的终点。下图为示意图。
第二种情况:特征序列的顶分型中,第一和第二元素间存在特征序列的缺口,如果从该分型最高点开始的向下一笔开始的序列的特征序列出现底分型,那么该线段在该顶分型的高点处结束,该高点是该线段的终点;特征序列的底分型中,第一和第二元素间存在特征序列的缺口,如果从该分型最低点开始的向上一笔开始的序列的特征序列出现顶分型,那么该线段在该底分型的低点处结束,该低点是该线段的终点。
强调,在第二种情况下,后一特征序列不一定封闭前一特征序列相应的缺口,而且,第二个序列中的分型,不分第一二种情况,只要有分型就可以。
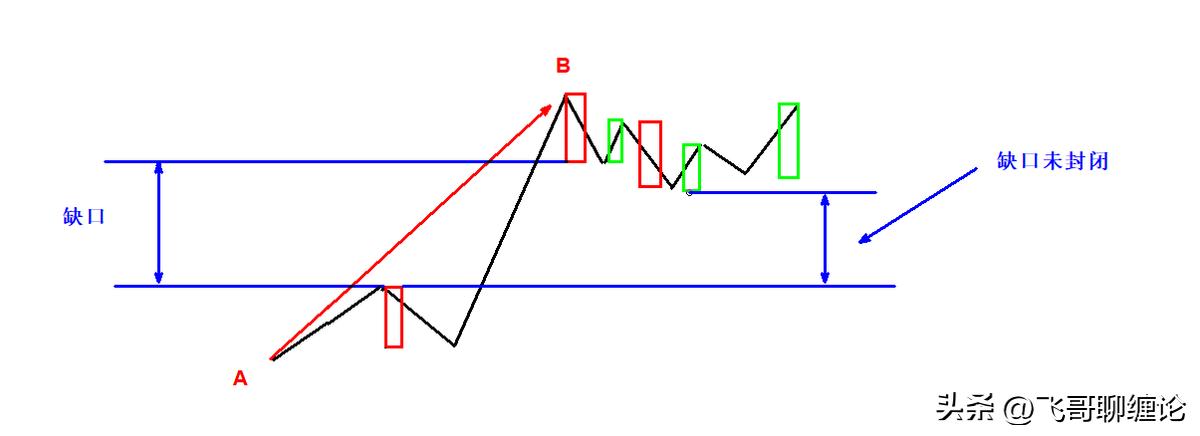
如上图,从A点开始的向上笔线段,特征序列的顶分型中,第一和第二元素间存在特征序列的缺口,B点开始的向下一笔开始的序列的特征序列出现底分型,那么A、B两点之间可以成线段。
如下图,为缠论原文里的图,前两个图形中标出了线段的划分。
发布者:股市刺客,转载请注明出处:https://www.95sca.cn/archives/730463
站内所有文章皆来自网络转载或读者投稿,请勿用于商业用途。如有侵权、不妥之处,请联系站长并出示版权证明以便删除。敬请谅解!






