关于朴素贝叶斯的简单理解，大家可以参考 https://blog.csdn.net/fisherming/article/details/79509025 ，很有趣的例子。

本文将通过股票的行业、市值、动量这三个维度的数据，利用伯努利分类器来预测下一日的涨跌幅情况，买入大概率会上涨的股票，看看这样的策略效果如何。具体一点就是：利用i日的特征和i+1的标签（收益率大于零）训练分类器，再利用i+1日的特征预测i+2日的标签，买入收益率大于零的股票。那么我们需要：

• 一、构建features数据
• 二、构建label数据
• 三、fit分类器和预测–策略主体
• 四、评价策略效果

就按照这个逻辑一步步来吧。

一、构建features数据

使用行业、市值、动量数据来构建features。

• 行业：是否在这个行业中，用哑变量。
• 市值：将具体数值转化为5分位中的数字（0，1，2，3，4），再转化为哑变量。
• 动量：用收盘价求出5日动量，再转化为分位数和哑变量。

预期的特征结果为：某只股票在某一天中，所处行业、市值分位、动量分位的特征为1，其余都为0。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.naive_bayes import BernoulliNB

# 读取行业数据
industry_data = pd.read_csv('INDUSTRY_GICS.csv',index_col=0,parse_dates=True,encoding='utf-8')
industry_data.head()

# 读取市值数据cap = pd.read_csv('MKT_CAP_ARD.csv',parse_dates=True,index_col=0)# 将市值对数化lcap = np.log(cap)# 读取交易量数据，用于排除停牌股票volume = pd.read_csv('VOLUME.csv',parse_dates=True, index_col=0)# 识别交易量为NAN值或0为股票停牌，设置对应时间股票市值数据为nan不参与后续分组，机器学习模型里面特征一般不允许是Nanlcap[((volume.isnull())|(volume==0))] = np.nan# 从2013年第一个交易日开始以后的数据lcap = lcap.loc['2013-01-04':]lcap.head()

# 将股票按照市值分成5组，每组中股票数量相等，使用到了pandas中qcut()函数labeled_lcap = lcap.apply(pd.qcut, axis=1, q=5, labels=False)labeled_lcap.head()

# 读取收盘价数据close = pd.read_csv('CLOSE.csv',parse_dates=True,index_col=0)# 识别交易量为NAN值或0为股票停牌close[(volume.isnull()) | (volume==0)] = np.nan# 计算5日动能mom = close/close.shift(5)-1# 去除缺失值mom.dropna(axis=0,inplace=True, how='all')mom = mom.loc['2013-01-04':]# 将股票按照动能分成5组，每组中股票数量相等, 按行去做；labeled_mom = mom.apply(pd.qcut, axis=1, q=5, labels=False)labeled_mom.head()

二、构建label数据

# 计算每日收益率close.sort_index(inplace=True)pct_change = close.pct_change()pct_change.dropna(axis=0,inplace=True, how='all')pct_change = pct_change.loc['2013-01-04':]pct_change.head()

labeled_pct_change = pct_change.copy()# 对于上涨的股票标记为1，下跌或涨幅为0的股票标记为0labeled_pct_change[labeled_pct_change > 0]=1labeled_pct_change[labeled_pct_change <= 0]=0labeled_pct_change.head()

# 读取成交量数据，用于制作交易日历；用于在循环的过程中，帮助我们控制具体的日期；volume_date = pd.read_csv('VOLUME.csv',index_col=0,parse_dates=True,usecols=[0])start_date = '2013-01-11'end_date='2017-01-01'# 取出回测范围内的交易日期，用于循环去控制日期；volume_date.sort_index(inplace=True)new_volume = volume_date.loc[start_date:end_date]trade_calendar = new_volume.indextrade_calendar

三、fit分类器和预测–策略主体

# 创建空Series用于储存策略收益率strategy_return = pd.Series(index=trade_calendar)

# 进行策略回测for i in range(len(trade_calendar)-2):    # 获取训练对应x，y数据的时间和预测时x，y数据的时间    train_x_time = trade_calendar[i]    train_y_time = trade_calendar[i+1]    predict_x_time = trade_calendar[i+1]    predict_y_time = trade_calendar[i+2]    # 模型训练用数据读取    # 由于伯努利分类器只看数据出现与否，所以下文中+200与+300是为了让特征区分开，否则lcap为1分位和mom为1分位将拥有相同的特征    train_data = pd.DataFrame(        {            'labeled_industry': industry_data.loc[train_x_time],            'labeled_lcap': labeled_lcap.loc[train_x_time]+200,            'labeled_mom': labeled_mom.loc[train_x_time]+300,            'labeled_pct_change':labeled_pct_change.loc[train_y_time]        }    )    train_data.dropna(axis=0, inplace=True, how='any')    # 生成训练用哑变量矩阵    dummy_data1 = pd.get_dummies(train_data['labeled_industry'])    dummy_data2 = pd.get_dummies(train_data['labeled_lcap'])    dummy_data3 = pd.get_dummies(train_data['labeled_mom'])    # 合并哑变量矩阵train_x    dummy_train_x = pd.concat([dummy_data1, dummy_data2, dummy_data3], axis=1)    # 模型预测用数据读取    predict_data = pd.DataFrame(        {            'labeled_industry': industry_data.loc[predict_x_time],            'labeled_lcap': labeled_lcap.loc[predict_x_time]+200,            'labeled_mom': labeled_mom.loc[predict_x_time]+300,            'pct_change': pct_change.loc[predict_y_time]        }    )    predict_data.dropna(axis=0, inplace=True, how='any')        #  生成预测用哑变量矩阵    dummy_predict_data1 = pd.get_dummies(predict_data['labeled_industry'])    dummy_predict_data2 = pd.get_dummies(predict_data['labeled_lcap'])    dummy_predict_data3 = pd.get_dummies(predict_data['labeled_mom'])    # 合并哑变量矩阵predict_x    dummy_predict_x = pd.concat([dummy_predict_data1, dummy_predict_data2, dummy_predict_data3], axis=1)    # 由于训练和预测的特征数量可能不同，所以需要columns的并集对列标签进行调整    character_union = dummy_train_x.columns.union(dummy_predict_x.columns)    dummy_train_x = dummy_train_x.reindex(columns=character_union, fill_value=0)    dummy_predict_x = dummy_predict_x.reindex(columns=character_union, fill_value=0)            # 训练模型    clf = BernoulliNB()    clf.fit(dummy_train_x.values, train_data['labeled_pct_change'].values)        # 进行预测并保存数据    prediction = clf.predict(dummy_predict_x.values)    predict_data['prediction'] = prediction    # 计算预测日策略收益率并保存到Series中    # 有可能某一天所有prediction都为0，    if predict_data['prediction'].sum() == 0:        strategy_return[predict_y_time] = 0    else:        strategy_return[predict_y_time] = np.average(predict_data['pct_change'], weights=predict_data['prediction'])

train_data.head()

dummy_train_x.head()

predict_data.head()

四、评价策略效果

# 收益曲线plt.figure(figsize=(10,6))plt.plot((strategy_return+1).cumprod(), label='strategy_return')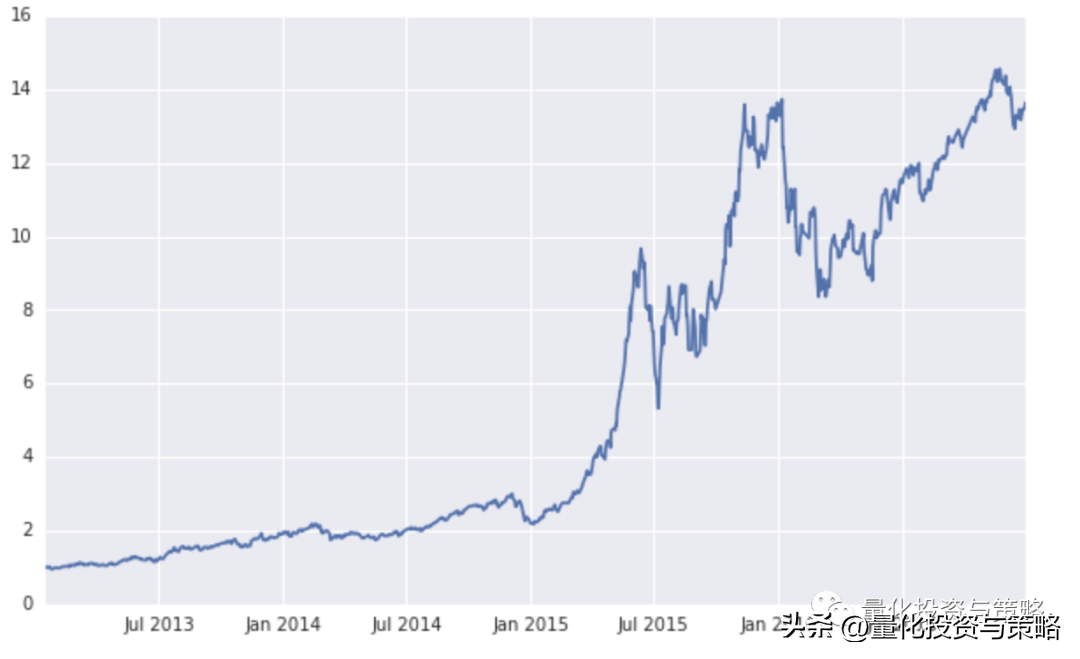

# 定义函数求各项回测指标def ratio(datas):    res = []    for item in datas:        data = datas[item]                # 累积收益率                strategy_cum = (data + 1).cumprod()        # 年化收益率        return_year = data.mean() * 252        # 每日收益率              return_avg = data.mean()         # 年化波动率        volatility = data.std() * 252 ** 0.5        # 最大每日收益        profit_max = data.max()        # 最大每日损失        loss_max = data.min()        # 信息比率                       ir = return_year / volatility        # 上涨天数        num_of_up = data[data > 0].count()        # 下跌天数        num_of_down = data[data < 0].count()        # 胜率        win_rate = float(num_of_up) / (num_of_up + num_of_down)        # 上涨时平均每日收益率        gain_of_up = data[data > 0].mean()        # 下跌时平均每日收益率                loss_of_down = data[data < 0].mean()        # 盈亏比        profit_loss_ratio = -(gain_of_up / loss_of_down)        # 最大回撤        drawdown = ((strategy_cum.cummax() - strategy_cum)/strategy_cum.cummax()).max()                # 创建一个临时的DataFrame        tmp = pd.DataFrame([ir, float((strategy_cum).tail(1)), return_year, return_avg, volatility, profit_max, loss_max,                              num_of_up, num_of_down, win_rate, gain_of_up, loss_of_down, profit_loss_ratio, drawdown],                            columns=[data.name],                            index=['Information Ratio', 'Cumulative Return', 'Annualised Return', 'Average return', 'Annualised Volatility', 'Maximum Daily Profit',                                   'Maximum Daily Loss', 'Number of Up Periods', 'Number of Down Periods', 'Win Rate', 'Avg Gain in Up Periods',                                   'Avg Loss in Down Periods', 'Profit and Loss Ratio', 'Maximum Drawdown'])        res.append(tmp)    # 返回拼接好的DataFrame    return pd.concat(res,axis=1,join='inner')

result = ratio(pd.DataFrame(strategy_return)).round(4)result.columns = ['strategy_return']result

可以看出，策略拥有相当不错的收益率，达到了77.67%，但是波动率和最大回撤也都在40%以上。

盈亏程度相当，胜率接近60%，也就是说总体而言预测正确的概率约为60%，还是不错的。

但是也存在很大的问题：每日换仓将导致巨大的手续费。